Assignment 6: Dynamic Programming
Learning Goals
- Implement a solution to a dynamic programming problem.
- Learn how to analyze and develop dynamic programming algorithms.
Grading
This assignment will be graded as pass/no-pass by a TA. To pass the assignment, you must
- Complete every question in the PDF and submit your answers to gradescope.
- Complete the programming component and submit your answers to gradescope.
- Meet with your TA during your learning community sessions. I prefer both partners to be present during the walk-through, but you can each meet with the TA separately if needed.
- Walk the TA through your answers. Do not expect to make corrections during the walk-through.
- The TA will then either
- mark your assignment as 100% on gradescope, or
- inform you that you have some corrections to make.
- If corrections are needed, then you will need to complete them and conduct a new walk-through with a TA.
If you have concerns about the grading walk-through, you can meet with me after you’ve first met with a TA.
Overview
This assignment includes two parts:
- Answer the question in this PDF.
- Write a program for the problem described in section The Jump-It Problem (must be compatible with Python 3.8).
You may work on this assignment alone or with a partner (I much prefer you to work with a partner). Please send me a message on Slack if you want me to assign you to work with a random partner. Whether you work alone or with a partner, only one partner will submit a both parts to gradescope.
Three key points:
- you should either print the PDF and write your answers directly on the printed sheet, or add annotations to the PDF with, for example, Edge (Windows) or Preview (OSX) (using the correct format and spacing will help us grade),
- ensure that the uploading partner adds the other partners after submission, and
- if you have any questions please ask them on Slack.
Example Execution
I always like to start by showing you the end result.
If you do not see an animation above this line (or if you see the animation but you don’t see the progress bar), you will need to refresh the page (sometimes more than once). Or you can go directly to the player: https://asciinema.org/a/370816
You can copy and past from the above animation!
The Jump-It Problem
In this assignment you will be implementing a dynamic programming solution to the Two-Dimensional Jump-It Problem (2D-JI). The 2D-JI problem is a board game optimization problem. Your program will output the optimal (minimal) cost of moving from the top-left cell to the bottom-right cell.
Moves
In the 2D-JI you are given a game board with \(m\) rows and \(n\) columns. You start at the top-left entry cell and you want to reach the bottom-right exit cell with a minimal cost. You are allowed to make the following moves:
- one cell right,
- one cell down,
- two cells right (jump over the cell to the right), or
- two cells down (jump over the cell below).
These moves assume that the cell you are moving into exists. For example, if you are in the second-to-last row you cannot perform move four (two cells down). Specifically, if you are in cell (1,1) (base index of 0) you can perform the following moves:
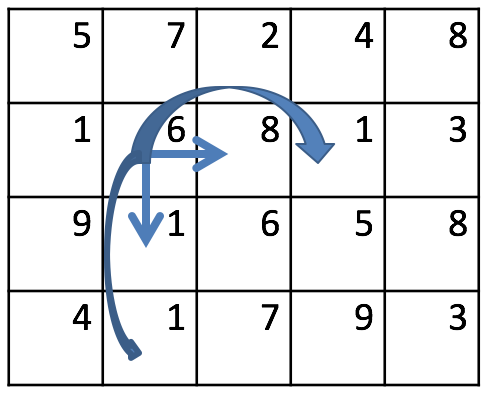
Below are three possible paths and costs for the above game board:
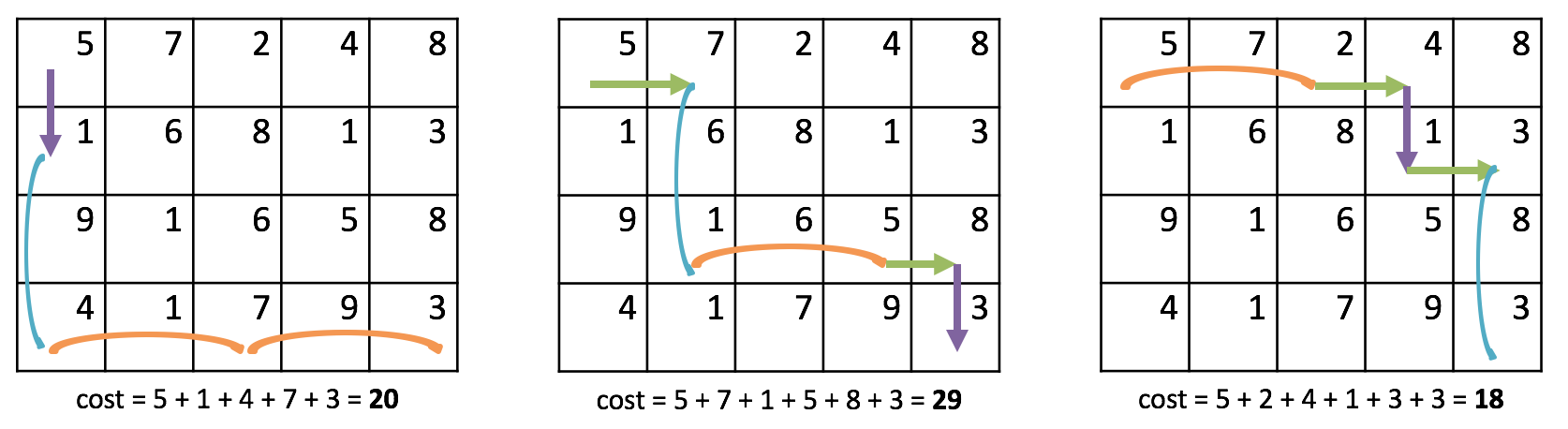
To solve this problem, you will be writing code for a dynamic programming algorithm. Essentially, you will be filling in a table of costs, where each cell in the costs table denotes the minimum cost of getting to the exit cell (bottom-right cell) from the current cell. For example, the cost table for the above game board looks like this:
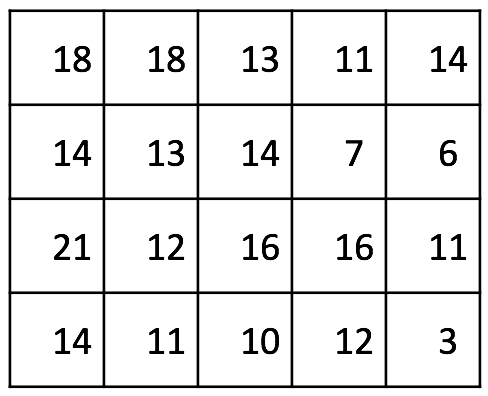
In the above table, you can see that it costs 3 to get to the exit cell from the exit cell. You can also see that it costs 11 to get to the exit cell from the cell above the exit cell, and that it optimally costs 18 to get to the exit cell from the entry cell.
The input file
Your programs will start by reading in the contents of a file, the name of which will be provided via a program argument (e.g., from the command line). The file will include all of the information needed to create a two-dimensional Jump-It game board:
m n
c11 c12 c13 ... c1n
c21 c22 c23 ... c2n
...
cm1 cm2 cm3 ... cmnWhere the first line gives values for \(m\) and \(n\), which are the number the number of rows and the number of columns, respectively. Each line after the first provides \(n\) integers for all of the values of a given row. Here is an example input file for the game boards shown above:
4 5
5 7 2 4 8
1 6 8 1 3
9 1 6 5 8
4 1 7 9 3Your program
Your source file should be named jumpit2d.py. You will be implementing a dynamic programming solution the the 2D-JI.
The 2D-JI problem is tricky because it has many edge cases to consider when developing the solution. You must account for the bounds of the cost table (you don’t want to go beyond the end of the table when moving or jumping). Specifically, you have 9 cases to handle when filling in the cost table:
If you are at the exit cell, then you cannot move.
If you are 1 cell to the left of the exit cell, then your only choice is to move right (into the exit cell).
If you are 1 cell above the exit cell, then your only choice is to move down (into the exit cell).
If you are 1 cell above and 1 cell to the left of the exit cell (the diagonal cell), then you have two choice: (a) go down and then right or (b) go right and then down.
If you are in the last row (and not at the exit cell or the cell to the left of the exit cell) then you need to consider two choices: (a) go right or (b) jump right. You should fill in these values starting at the cell 2 to the left of the exit cell, working your way to the first cell in the last row.
If you are in the last column (and not at the exit cell or the cell above the exit cell) then you need to consider two choices: (a) go down or (b) jump down. You should fill these values in starting at the cell 2 above the exit cell, working your way to the first cell in the last column.
If you are in the second-to-last row (and not at the diagonal cell or the last cell in the row), then you need to consider three choices: (a) go down, (b) go right, or (c) jump right.
If you are in the second-to-last column (and not at the diagonal cell or the last cell in the column), then you need to consider three choices: (a) go right, (b) go down, or (c) jump down.
Finally, for all other cells you must consider four cases: (a) go right, (b) jump right, (c) go down, or (d) jump down.
In all cases, you should take the value of the board at the current cell and add it to the minimum value for all choices in the cost table. As you can see, we are filling in the cost table starting at the exit cell (bottom-right) and moving our way up to the entry cell (top-left).
I’d encourage you to work through these 9 cases individually. Once you have done that, you should think of some ways to reduce all of these cases into a single double-nested for-loop (hint: you can add “padding” around the table with certain values that eliminate the need for handling all of these cases separately).
Once you have the final table, you must print the value in the entry cell of the cost table.
I’d encourage you to first try implementing this program from scratch. But I am also providing this skeleton code to help you get started if you are stuck.
Submitting Your Assignment
You will submit your PDF assignment on gradescope. Only one partner should submit your PDF. The submitter will add the other partner through the gradescope interface.
To pass the autograder, your output must exactly match the expected output. Your program output should be similar to the example execution above, and the autograder on gradescope will show you the correct output if yours is not formatted properly. You can use text-compare to compare your output to the expected output and that should give you an idea if you have a misspelled word or extra space (or if I do).
Additional details for using gradescope can be found here: