Week 11: Trees and Search

• How to Learn Tree Data Structures the Codeless Way
  • This is a good overview of what trees are and why they're interesting
• Data Structures: Trees
  • This video focuses on binary trees and searching for numbers in such trees
  • It's just one example of using trees with special structure

• Search 1
• Search 2

A tree can be defined recursively as a vertex (or "node") with zero or more edges, each of which points to another (different) tree. Here are some trees:

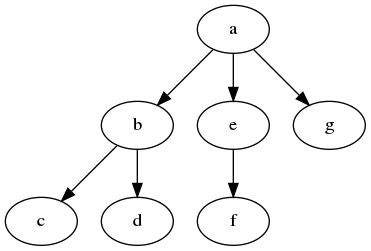
Every tree has a root and one or more leaves (and zero or more "inner nodes"), connected by edges. In a single-element tree the root is a leaf (elements—the little circles—are often called nodes or vertices [singular "vertex"]). Also, you may have noticed that computer scientists traditionally draw trees with the roots on top; some of us don't go outside much so this is our educated guess of how trees work. Because we like to mix metaphors, we say that a node's parent is the one connected to it, and its children are the ones it's connected to. The root node has no parent and leaves have no children. Basically there's a lot of jargon here, but you'll get used to it.

We could represent a tree as a list of lists, but since we might want each node to hold a value we'll instead make a Node class:

class Node:
  def __init__(self, value, children:List[Node]):
    self.value = value
    self.children = children

We can traverse a tree to visit all its nodes in some order; one way of thinking of this operation is that it turns a non-linear tree into a linear list. We group these into two main categories: breadth-first (or "level by level") and depth-first (or "branch-at-a-time") traversals. In both cases we'll assume that we prefer children which are visually further left before the ones visually further right, but other child orderings are possible.

In a breadth-first traversal, we start with the root node. We add each of its children to the list of nodes to visit next; then we visit each of those in turn, adding their children to that list. This list operates like a queue (which we mentioned in week 9's notes). When our list is empty we will have visited every node. We might write breadth-first traversal like this:

def breadth_first_traversal(root:Node) -> List:
    nodes = []
    queue = [root]
    while queue: # implicitly, while queue.len() > 0
        first = queue.pop(0) # removes first element and returns it
        nodes.append(first.value)
        for child in first.children:
            queue.append(child)
    return nodes

• Considering tree 2, in what order will the nodes be visited by a breadth-first traversal?
• Challenge problem: Is it true that this will only visit nodes in increasing "height" order, i.e. it will visit all nodes with \(k\) ancestors before it visits any node with \(k+1\) ancestors? Why?

It's most natural to phrase depth-first traversal recursively:

def depth_first_traversal(root:Node) -> List:
    here = [root.value]
    for node in root.children:
        here += depth_first_traversal(node)
    return here

The main orderings for depth-first traversals are preorder (parents before children, as above) and postorder (leaves first, then their parents—how would you change the sample above to use postorder traversal?). If the children of a node and the node itself can be compared (with e.g., <) then there is also an inorder traversal where the sorted children are visited up until the last one lesser than the parent; then the parent is visited; and finally the remaining children are visited.

• What's the base case of the recursion above?
• Considering tree 2, in what order will the nodes be visited by a depth-first preorder traversal?

Even though the recursive definition of depth-first search is elegant, it might be illustrative to use this iterative version:

def depth_first_traversal_iterative(root:Node) -> List:
    nodes = []
    stack = [root]
    while stack: # implicitly, while stack.len() > 0
        first = stack.pop() # removes last element and returns it
        nodes.append(first.value)
        for child in first.children:
            stack.append(child)
    return nodes

Notice how similar it looks to the breadth first traversal!

• Is this a preorder or postorder traversal?
• Challenge problem: Imagine we are currently visiting a node A with two children, B and C. Will this really visit all the descendants of B before visiting C? If so, why? If not, why not?

Search is, put glibly, the problem of finding a needle in a haystack. We've already seen one simple type of search problem: is a number \(n\) present in a list of numbers? To solve that, we just checked \(n\) against every number in the list. Unfortunately, not all search problems are so simple.

In general a search problem is defined by a starting state, a goal condition, and a rule for coming up with possible next states from the current state. The assumption we're making is that we can capture everything interesting about the "world" of the search problem in a data structure called a search state. Every possible configuration of the world is represented by a search state, and from each state we can reach zero or more successor states.

In the concrete example of maze solving in the search slides linked above, a search state is just the position of the character in the maze; the initial state has the character at the entrance and the goal condition is whether the character has reached the exit of the maze. From a given state, there are up to four successor states (moving to the right, left, up, or down, except for those directions forbidden by walls).

We can imagine that if each search state were a node in a tree, the rule for finding successor states describes the children of that node. Then, solving the search problem amounts to a tree traversal problem: if we traverse the nodes of the tree, do we eventually hit a node satisfying the goal condition? Here's the depth first traversal from above refitted for search:

def depth_first_search(state:SearchState) -> bool:
    if is_goal_state(state):
        return True
    for next_state in successor_states(node):
        if depth_first_search(next_state):
            return True
    return False

Now, it stands to reason that we might want to know what series of steps takes us to the goal state, or what the goal state is like:

def depth_first_trace(state:SearchState) -> List[SearchState]:
    if is_goal_state(state):
        return [state]
    for next_state in successor_states(node):
        path = depth_first_search(next_state)
        if path.len() > 0:
            return [state]+path
    return []

Finally, to test out your understanding, look at the "N-queens problem" from the second set of search slides. Try to answer the questions at the end of the slides—you could double check your answers with your mentor group!