

|
CS 334
|
Dijkstra: Originally we were obligated to write programs so that a computer could execute them. Now we write the programs and the computer has the obligation to understand and execute them.
Progress in programming language design marked by increasing support for abstraction.
Computer at lowest level is set of charged particles racing through wires w/ memory locations set to one and off - very hard to deal with.
In computer organization look at higher level of abstraction: interpret sequences of on/off as data (reals, integers, char's, etc) and as instructions.
Computer looks at current instruction and contents of memory, then does something to another chunk of memory (incl. registers, accumulators, program counter, etc.)
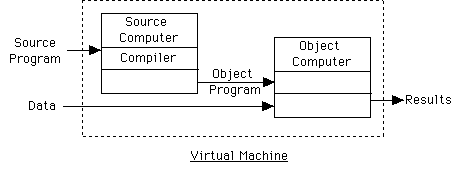
When write Pascal (or other language) program - work with different virtual machine.

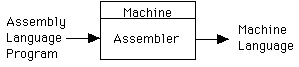
Compiler:
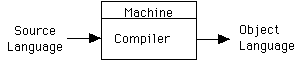
Preprocessor:

Execution of program w/ compiler:
Interpreter:
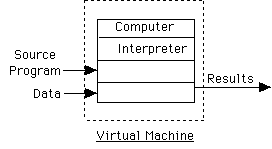
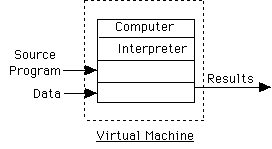
We will speak of virtual machine defined by a language implementation.
Machine language of virtual machine is set of instructions supported by translator for language.
Layers of virtual machines on Mac: Bare PowerPC chip, OpSys virtual machine, Lightspeed Pascal machine, application program's virtual machine.
We will describe language in terms of virtual machine
Slight problem:
Problem : How can you ensure different implementations result in same semantics?
Sometimes virtual machines made explicit:
Two extreme solutions:
Pure interpreter: Simulate virtual machine (our approach to run-time semantics)
REPEAT
Get next statement
Determine action(s) to be executed
Call routine to perform action
UNTIL done
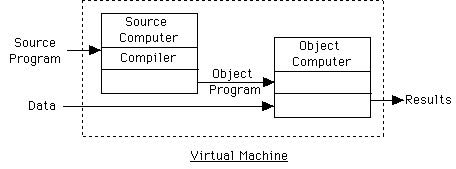
Pure Compiler:
| compiler | interpreter |
|---|---|
| Only translate each statement once | Translate only if executed |
| Speed of execution | Error messages tied to source More supportive environment |
| Only object code in memory when executing. May take more space because of expansion | Must have interp. in memory when executing (but source may be more compact) |
Rarely have pure compiler or interpreter.
In FORTRAN, Format statements (I/O) are always interpreted.
for i := .. do ...
for j:= 1 to n do
A[i,j] := ....
Like to have easily portable compilers
First used in ALGOL 60 Report - formal description
Generative description of language.
Language is set of strings. (E.g. all legal ALGOL 60 programs)
<expression> -> <term> | <expression> <addop> <term>
<term> -> <factor> | <term> <multop> <factor>
<factor> -> <identifier> | <literal> | (<expression>)
<identifier> -> a | b | c | d
<literal> -> <digit> | <digit> <literal>
<digit> -> 0 | 1 | 2 | ... | 9
<addop> -> + | - | or
<multop> -> * | / | div | mod | and
The items in pointy brackets (<...>) are called
non-terminals of the grammar. Each non-terminal has one or more associated
productions where it is to the left of the arrow. Where a non-terminal can
be rewritten according to several different rules, the different right hand
sides may be separated by "|". To generate an expression, start with
<expression> and replace it by one of the right sides of its
rule. Continue replacing non-terminals by a right side of its production
until no non-terminals are left. The result is said to be generated from
the initial non-terminal.
For example, <expression> generates: a + b * c + b. See the text for pictures of parse trees.
The grammar gives precedence and which direction that op's associate.
Extended BNF handy:
item enclosed in square brackets is optional
<conditional> -> if <expression> then <statement> [ else <statement> ]
item enclosed in curly brackets means zero or more occurrences
<literal>-> <digit> { <digit> }
Syntax diagrams - alternative to BNF. See section 9.6 of Ullman for
ML syntax diagrams.
Syntax diagrams are never recursive, use "loops" instead.
<statement> -> <unconditional> | <conditional>How do you parse:<unconditional> -> <assignment> | <for loop> |
"{" { <statement> } "}"
<conditional> -> if (<expression>) <statement> |
if (<expression>) <statement> else <statement>
if (exp1)
if (exp2)
stat1;
else
stat2;
Could be
if (exp1)
{
if (exp2)
stat1;
else
stat2;
}
or
if (exp1)
{
if (exp2)
stat1;
}
else
stat2;
Ambiguous
Pascal, C, and Java rule: else attached to nearest then
To get second form, include "{,}" as shown above..
MODULA-2 and ALGOL 68 require "end" to terminate conditional:
Why isn't it a problem in ML?
Ambiguity in general is undecidable
Chomsky developed mathematical theory of programming languages:
Not all aspects of programming language syntax are context-free.
The formal specification of the syntax of a language can be used to help write lexical scanners and parsers for a programming language. The lexical scanner and parser that I provided for the last homework is an example of how this can be done. (Ignore the signature and structure information -- we will talk about that later.)
Evaluating lex file first opens a file, inputs the contents, and then explode's it into a list of characters. The function gettokens converts the list of characters into a list of tokens with type
datatype token = ID of string | NUM of int | Plus | Minus | Mult | Div | Neg | LParen | RParen | EOF;
The code for gettokens is straightforward, so I will simply let you take a look at it.
Section 4.6 of the text, starting on page 4-20, provides an extended discussion of recursive descent parsing, with an extended example of parsing arithmetic expressions in C. Please read that and compare the parser in ML with that given in C (note that the C program also evaluates the arithmetic expression, while you of course wrote a separate function to evaluate the expressions).
Here we will examine parsing using XML as our example. XML is a "hot" topic these days. XML stands for extensible markup language. HTML for making web pages is an example of a standard generalized mark-up language (SGML), while XML can be seen as being more general than HTML, but not as rich as SGL. The key difference between XML and HTML is that XML is a meta-language (the tags are not fixed - either in syntax or semantics) that is designed so that richly structured documents could be sent over the web, whether or not those documents were designed to be displayed. Thus an XML document might be used to transfer information across the internet from one computer to another in such a way that a program on one computer could generate the data, while the other could read it and operate on it.
The hope is that standards will be created for different kinds of information to be transmitted. Then anyone wishing to transfer that kind of information will use the same format.