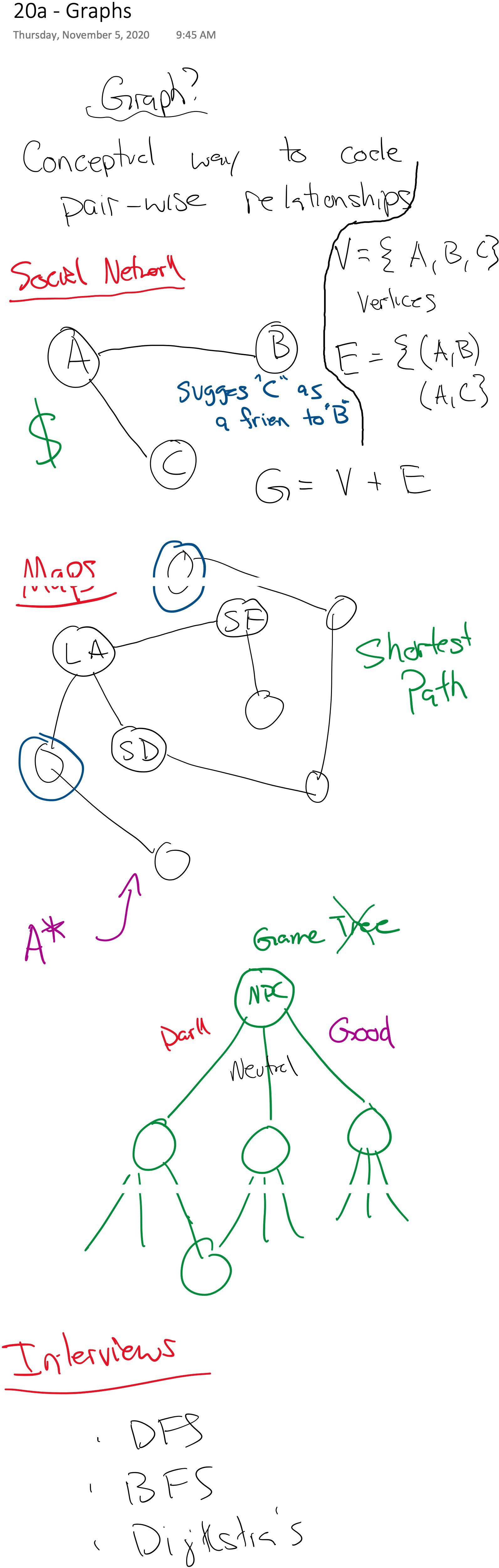
**Graph Basics** *Nov 5* # Graphs Graphs are a mathematical model comprising a set of vertices and a set of edges. $$ G = (V, E) $$ where $V$ is a set of vertices and $E$ is a set of edges. In class, someone asked a question about gaming and graphs/trees. I couldn't think of the term, but this is what I was trying to describe: [Behavior Trees](https://en.wikipedia.org/wiki/Behavior_tree_(artificial_intelligence,_robotics_and_control)).  # Graph Terms Undirected : edges do not have a direction; $(A, B)$ is the same as $(B, A)$ Directed : edges point in a specific direction; from one vertex to another Weighted : edges have an associated weight/cost Adjacent : two vertices are adjacent if they are connected by an edge Incident : an edge is incident to a vertex if it is connected to the vertex Degree : the degree of a vertex is counted as its number of incident edges In-degree : (for directed graphs) the number of edges pointing to a given vertex Out-degree : (for directed graphs) the number of edges pointing away from a given vertex Path : a sequence of vertices ($v_1$, $v_2$, ..., $v_k$) where there exists an edge connected each adjacent vertex ($(v_1, v_2)$, $(v_2, v_i)$, ..., $(v_j, v_k)$) and there are not repeated edges Cycle : a path where the first and last vertex are the same Acyclic : a graph that does not contain any cycles Connected : (for undirected graphs) a graph in which all vertices are connected by a path Strongly Connected : (for directed graphs) a graph in which all vertices are connected by a path Weakly Connected : (for directed graphs) a graph in which all vertices are connected if edges are replaced with undirected edges Tree : a directed, acyclic graph that is connected and has a special vertex known as the root DAG : shorthand for a directed, acyclic graph Complete : a graph with an edges between every pair of vertices # Graph Characteristics and Types