**Heaps, Priority Queues, and HeapSort**
*Oct 22*
# Administrivia
- Questions on the quiz?
- Midterm 2 review next Tuesday
- Midterm 2 next Wednesday (same format)
# Heaps
Heaps are binary trees (**not** binary search trees) that come in two flavors:
- **Min**-Heaps: each node's key is **smaller** than or equal to its children's keys
- **Max**-Heaps: each node's key is **greater** than or equal to its children's keys
*Where is the minimum value in a min-heap?* **At the root.**
*Where is the maximum value in a min-heap?* **At a leaf.**
*Where is the maximum value in a max-heap?* **At the root.**
*Where is the minimum value in a max-heap?* **At a leaf.**
Our first max-heap:
**********************************
* .-.
* | 9 |
* +-+
* / \
* / \
* / \
* / \
* .+. .+.
* | 8 | | 3 |
* +-+ +-+
* / \ / \
* .+. .+. .+. .+.
* | 7 | | 5 | | 1 | | 2 |
* +-+ '-' '-' '-'
* / \
* .+. .+.
* | 6 | | 4 |
* '-' '-'
**********************************
Notice that the heap does not have any unique order to it. For example, the number `3` appears in the second level but it could also appear further down the tree (e.g., swap the `3` and the `6`).
# Heap Representation
Unlike a binary search tree, we will not be using a node class and points for links among nodes. Instead, we will be using an `array`. The array representation is faster and uses less memory!
The graph above would be represented with this array:
~~~text
[ 9, 8, 3, 7, 5, 1, 2, 6, 4 ]
~~~
For a node at index $k$:
- its children are at $2k + 1$ and $2k + 2$
- its parent is at index $\lfloor\frac{k-1}{2}\rfloor$
$k$ | Left Child | Right Child | Parent
:--:|:----------:|:-----------:|:------:
0 | 1 | 2 | None
1 | 3 | 4 | 0
2 | 5 | 6 | 0
3 | 7 | 8 | 1
4 | 9 | 10 | 1
5 | 11 | 12 | 2
6 | 13 | 14 | 2
7 | 15 | 16 | 3
# Bubbling
If a node is not in the correct place (for example, after an insertion or deletion). You must move it up or down the tree, which corresponds to left or right in the array, respectively. This process is often called **bubbling** (or swimming or promoting/demoting or percolating).
Bubbling up (left) the tree corresponds to swapping an element with its parent. And bubbling down (right) the tree corresponds to swapping an element with one of its children.
From here on, I will refer to bubbling-left or bubbling-right so that it is easier to picture moving an element in the array.
*How many comparisons for bubble left?* **At most $log(n) + 1$**
*How many comparisons for bubble right?* **At most $log(n) + 1$**

# Heap Complexity
Running Time:
- Insert is $O(log(n))$
- Extract-Max (or min) is $O(log(n))$
Memory:
- Uses $O(n)$ memory and no extra memory is needed during insertions or deletions
# Priority Queue
Maintain a queue for which you can always get the maximum (or minimum) element. For example, in handling processes on a computer (execute the highest priority process first), or visiting with patients in order of severity (visit the most ill patients first).
## Unsorted Array
A *naive* approach to solving this problem:
1. Use an unsorted array.
2. Insert elements at the end of the array: $O(1)$.
3. Extract the max by searching through the array: $O(n)$.
For example, let's insert letters into a max priority queue that has a capacity of 10:
```
Inserted 'P': [ P, ∅, ∅, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'Q': [ P, Q, ∅, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'E': [ P, Q, E, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Extracted 'Q': [ P, E, ∅, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'X': [ P, E, X, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'A': [ P, E, X, A, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'M': [ P, E, X, A, M, ∅, ∅, ∅, ∅, ∅ ]
Extracted 'X': [ P, E, M, A, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'P': [ P, E, M, A, P, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'L': [ P, E, M, A, P, L, ∅, ∅, ∅, ∅ ]
Inserted 'E': [ P, E, M, A, P, L, E, ∅, ∅, ∅ ]
Extracted 'P': [ E, E, M, A, P, L, ∅, ∅, ∅, ∅ ]
```
## Sorted Array
Another *naive* approach to this problem is to:
1. Use a sorted array.
2. Insert elements in the correct position: $O(n)$ (we have to shift everything to the right).
3. Extract the max by taking the last element: $O(1)$.
For example, let's insert letters into a max priority queue that has a capacity of 10:
```
Inserted 'P': [ P, ∅, ∅, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'Q': [ P, Q, ∅, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'E': [ E, P, Q, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Extracted 'Q': [ E, P, ∅, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'X': [ E, P, X, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'A': [ A, E, P, X, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'M': [ A, E, M, P, X, ∅, ∅, ∅, ∅, ∅ ]
Extracted 'X': [ A, E, M, P, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'P': [ A, E, M, P, P, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'L': [ A, E, L, M, P, P, ∅, ∅, ∅, ∅ ]
Inserted 'E': [ A, E, E, L, M, P, P, ∅, ∅, ∅ ]
Extracted 'P': [ A, E, E, L, M, P, ∅, ∅, ∅, ∅ ]
```
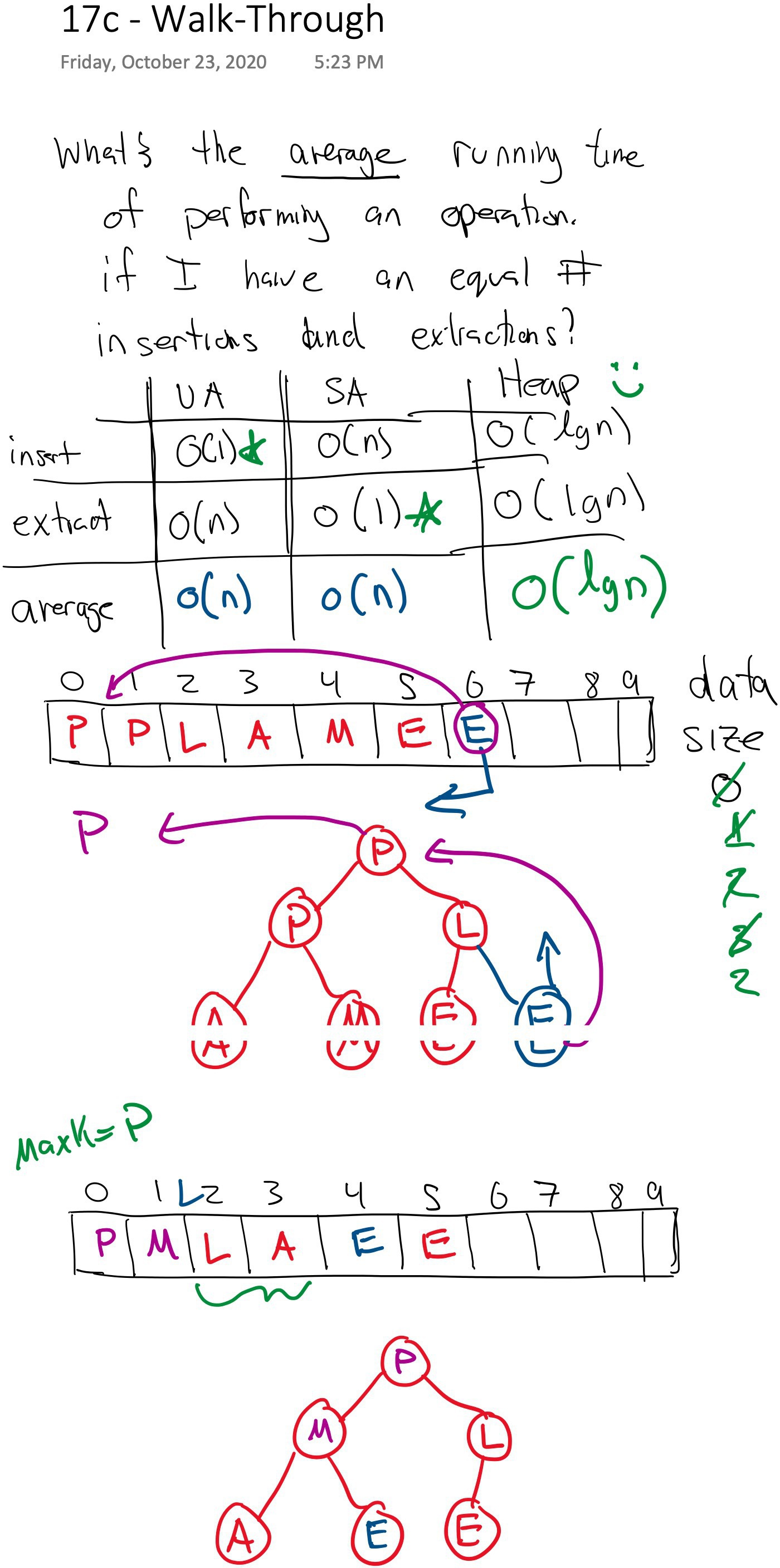
## Binary Heap
*What average operation running time of the previous two approaches if we are doing an equal number of `insert` and `extractMin` calls?* **Average is $O(n/2)=O(n)$**
To bring this average down, we can:
1. Use a max binary heap.
2. Insert items in $O(log(n))$
3. Extract the max item in $O(log(n))$
For an average operation running time of $O(log(n))$.
For example, let's insert letters into a max priority queue that has a capacity of 10:
```
Inserted 'P': [ P, ∅, ∅, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'Q': [ Q, P, ∅, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'E': [ Q, P, E, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Extracted 'Q': [ P, E, ∅, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'X': [ X, E, P, ∅, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'A': [ X, E, P, A, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'M': [ X, M, P, A, E, ∅, ∅, ∅, ∅, ∅ ]
Extracted 'X': [ P, M, E, A, ∅, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'P': [ P, P, E, A, M, ∅, ∅, ∅, ∅, ∅ ]
Inserted 'L': [ P, P, L, A, M, E, ∅, ∅, ∅, ∅ ]
Inserted 'E': [ P, P, L, A, M, E, E, ∅, ∅, ∅ ]
Extracted 'P': [ P, M, L, A, E, E, ∅, ∅, ∅, ∅ ]
```
# Heap Sort
1. Build a heap (min or max? does it matter?).
2. Repeatedly move the max to the end and bubble the rest of the heap.
I've added this functionality to the `MaxHeap` class, which you can find [in the lecture code repository](https://github.com/pomonacs622020fa/LectureCode/blob/master/Heaps/MaxHeap.java). It is a pretty **poor** place to put this code, but I'd rather have it all in one file for the purpose of demonstration.
First, I added an extra constructor that takes in a potentially unsorted array.
~~~java linenumbers
public MaxHeap(Key[] items) {
data = items;
size = items.length;
heapify();
}
~~~
Next, I added a `heapify` method that efficiency takes an unsorted array and turns it into a valid heap.
~~~java linenumbers
private void heapify() {
// Bubble non-leaves to the right
for (int k = size / 2; k >= 0; k--) {
bubbleRight(k);
}
}
~~~
The running time of `heapify` is $O(n)$. Alternatively, we could have just inserted $n$ elements into the heap. *What is the running time of inserting n elements?*
It is tempting to think that `heapify` should take $n/2 * O(lg(n))$ time. Since we are calling `bubbleRight` $n/2$ times. If you'd like to see in more detail why it is actually $O(n)$ I'd encourage you to take a [look at the math here](https://www.geeksforgeeks.org/time-complexity-of-building-a-heap/).
Finally, all we have left to do is sort.
~~~java linenumbers
public void sort() {
int originalSize = size;
while (size > 0) {
swap(0, --size);
bubbleRight(0);
}
size = originalSize;
}
~~~
First, I should note that sorting like this will invalidate the heap, which is why I made the comment above about my coding practice here being poor.
Next, you can see that we are repeatedly swapping the maximum element (the item at index `0`) to the end of the current subarray (from `0 ..< size`) and then bubbling the swapped item right. You can view this as repeatedly extracting the maximum element and putting it at the end of the subarray.
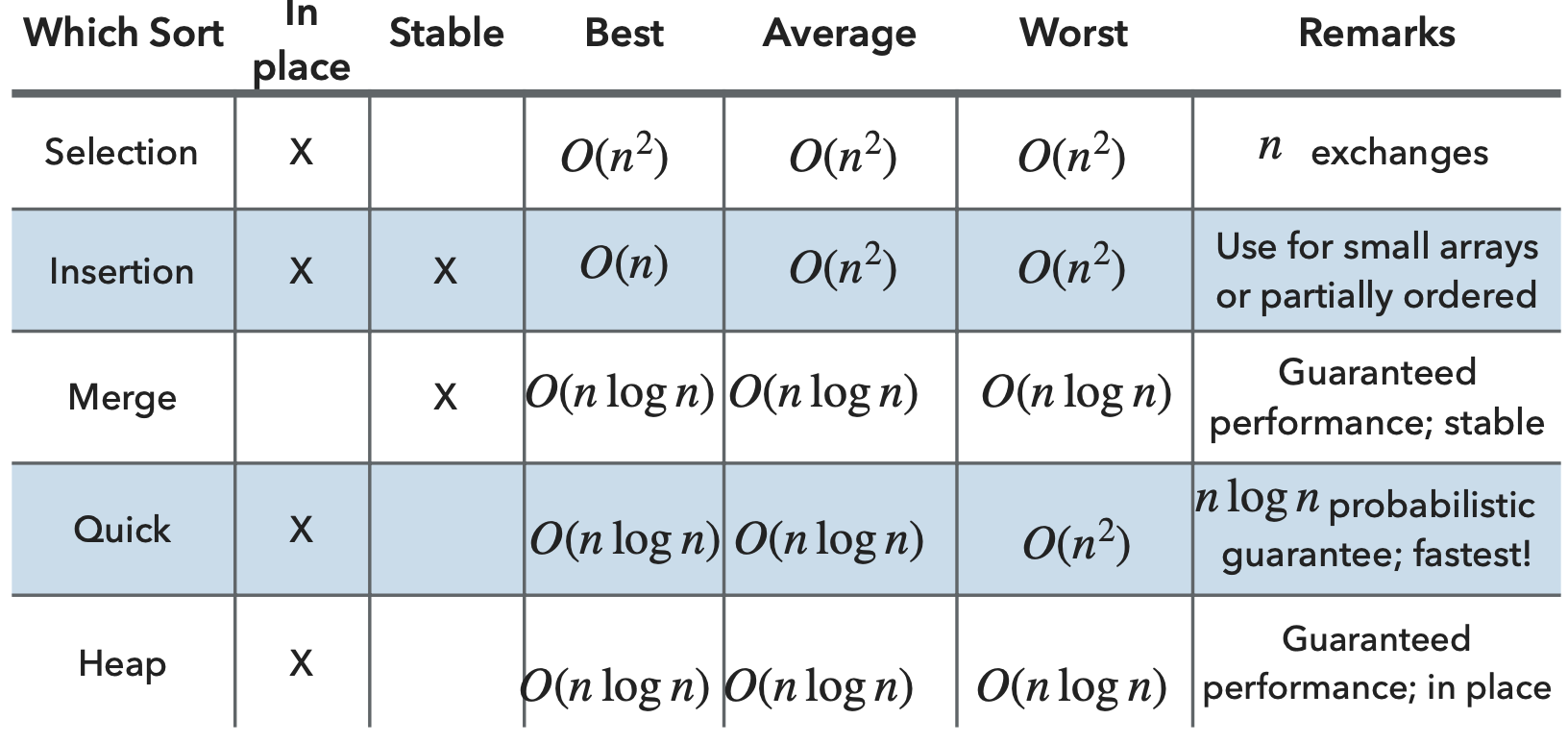
**Heapsort summary**:
- Heapify takes $O(n)$.
- Sorting calls bubble right $n$ times for a total amount of work equal to $O(n log(n))$.
- This is an in-place algorithm
- This is not a stable algorithm
# Code Walk-Through