**Binary Trees**
*Oct 20*
# Administrivia
- On-disk sort due today
- Midterm 2 review next Tuesday
- Midterm 2 next Wednesday (same format)
# The Story So Far
We first discussed basic data structures:
- Arrays
- Resizing arrays (ArrayLists)
- LinkedLists
- Queues
- Stacks
We looked at the running time and memory usage for each data structure.
We then discussed sorting:
- Selection sort
- Insertion sort
- Mergesort
- Quicksort
We looked at the number of comparisons and swaps, stability, and memory usage (in-place or not) for each algorithm.
Along the way we also discussed comparisons (the `Comparable` and `Comparator` interfaces) and iteration (the `Iterable` interface).
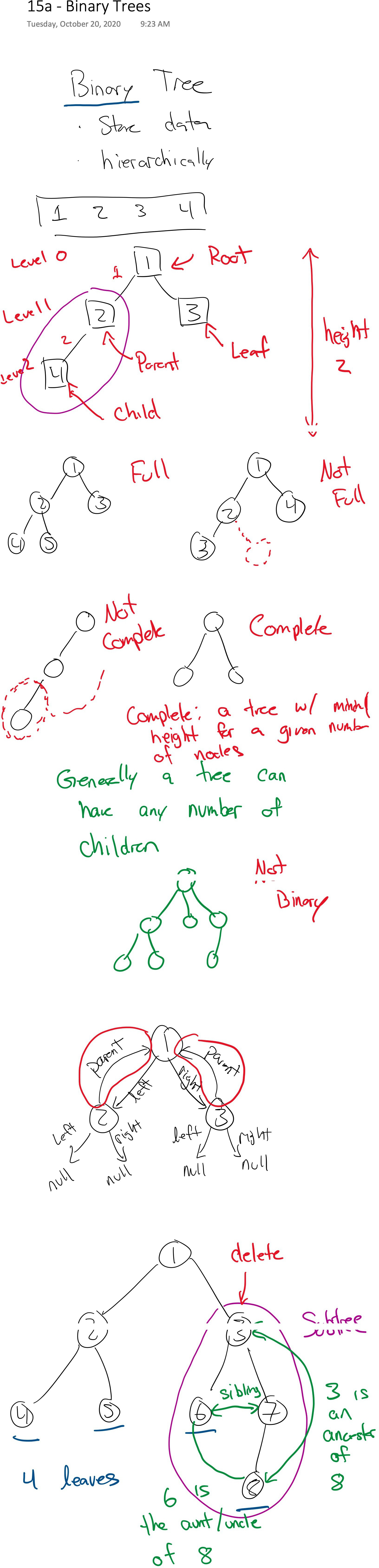
# Binary Trees
Store elements hierarchically rather than linearly. For example, consider your computer's file system--all files are stored in directories and sub-directories, with your user directory being at the root of your user files.
A **tree** is a set of nodes that store elements based on a parent-child relationship. You can think of it as a linked list where each node as 0 or more `next` nodes.
Some helpful definitions:
Root
: node at the base (top) of the tree (similar to the head node of a linked list)
Parent
: of a specific node is the node directly above another node
Child
: of a specific node is the node directly below another node
Leaf
: node without any children
Height
: of a tree is the length of the longest path from the root to a leaf
Level
: the root is at level 0, all other nodes at at a level $= L_{parent} + 1$ (aka depth)
Full
: a tree where every node has 0 or the maximum number of possible children
k-Ary
: a tree in which each node has a maximum of k children
Complete
: a k-ary tree in which all leaves have the same depth and all internal nodes have degree k.
A **binary tree** is a tree where every node can have 0, 1, or **2** children.
# Binary Tree Code
The code below is also found [here on GitHub](https://github.com/pomonacs622020fa/LectureCode/blob/master/BinaryTrees/BST.java).
~~~java linenumbers
public class BinaryTree- {
private class Node {
private Item item;
private Node left;
private Node right;
public Node(Item item, Node left, Node right) {
this.item = item;
this.left = left;
this.right = right;
}
public Node(Item item) {
this(item, null, null);
}
}
private Node root;
}
~~~
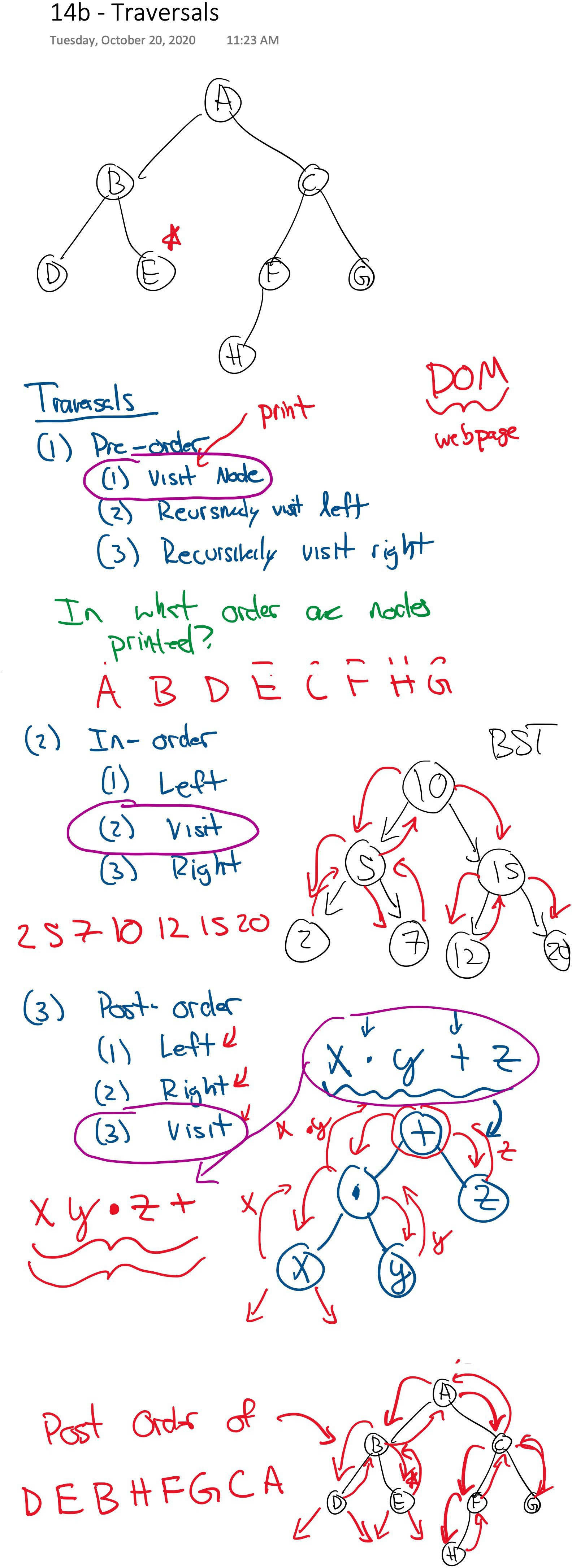
# Tree Traversals
- Pre-order
- In-order
- Post-order
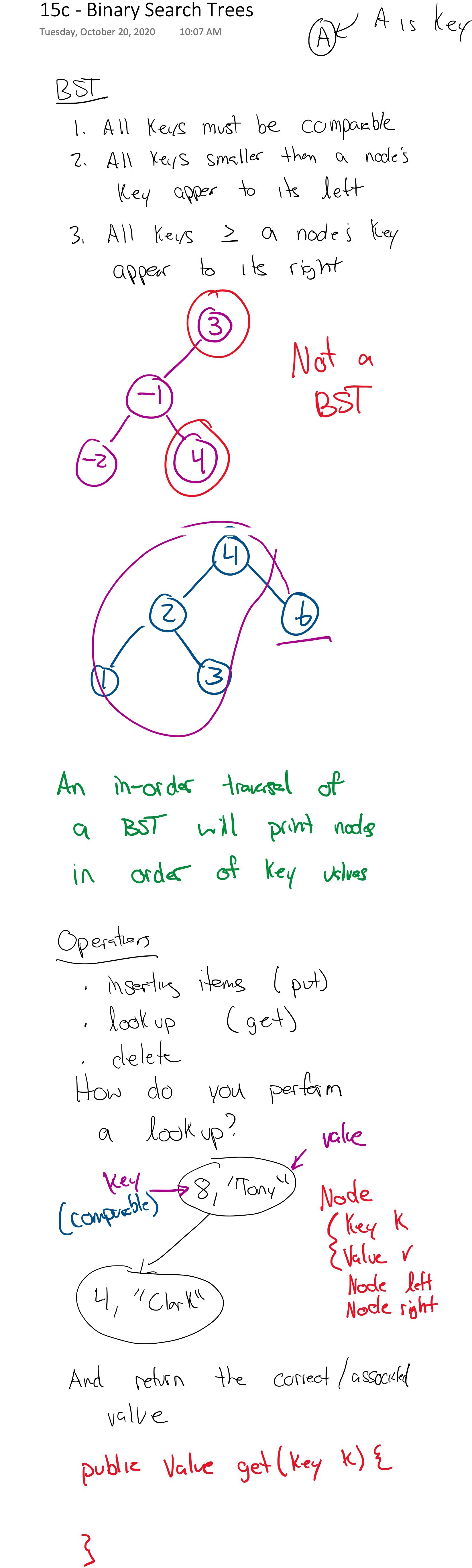
# Binary Search Trees (BSTs)
[Code for BST](https://github.com/pomonacs622020fa/LectureCode/blob/master/BinaryTrees/BST.java).
A binary tree where items appears in a particular "order".
Binary search tree property:
1. Each node has a `Comparable` **key** and a **value** with no restrictions
2. All keys smaller to node's key appear to its left
3. All keys larger (or equal) to a node's key appear to its right
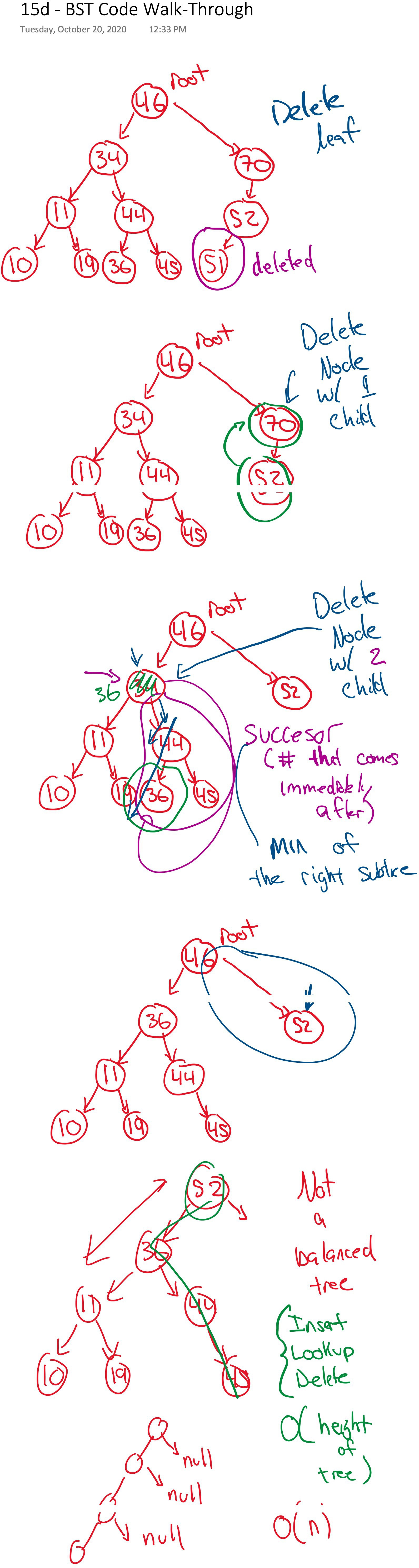
Take a careful look at the BST `put` and `delete` methods. What is the running time? To help, consider the case when you insert these nodes in order: `1, 2, 3, 4, 5` (assume that the keys and values are the same).
**********************
* .-.
* | 1 |
* +-+
* \
* .+.
* | 2 |
* +-+
* \
* .+.
* | 3 |
* +-+
* \
* .+.
* | 4 |
* +-+
* \
* .+.
* | 5 |
* '-'
**********************
The number of nodes in the tree is typically denoted with $n$.
What is the running time of a searching for the `5`?
**Answer**: $O(n)$
*For an unbalanced tree--a tree where the left and right subtrees have drastically different heights--the running time of nearly all operations becomes **linear***.
Now consider this example:
*****************
* .-.
* | 2 |
* +-+
* / \
* .+. .+.
* | 1 | | 4 |
* '-' +-+
* / \
* .+. .+.
* | 3 | | 5 |
* '-' '-'
*****************
What is the running time of finding the `5`? We no longer need to look at all nodes. We
1. Start at the root (`2`) and go right
2. Go right from the `4`
3. Find the `5`
We are eliminating **half** of the tree each time. Thus the running time for searching a balanced tree is $O(log_2(n))$.
# BST Code Walk-Through
# Balanced Trees
A number of methods exist for keeping the tree *balanced*. Balanced means that the height of the tree is $O(log_2(n))$--and thus, most operations take $O(log_2(n))$.
**Your are not required to know how balancing works, just that it is possible and why it is useful.**
- [Red-black trees](https://en.wikipedia.org/wiki/Red%E2%80%93black_tree)
- [AVL trees](https://en.wikipedia.org/wiki/AVL_tree)
- [2-3 trees](https://en.wikipedia.org/wiki/2%E2%80%933_tree) and [slides](lecture24-balanced_search_trees.pdf)
- [B-trees](https://en.wikipedia.org/wiki/B-tree)
- [Splay trees](https://en.wikipedia.org/wiki/Splay_tree)
- [etc.](https://en.wikipedia.org/wiki/Self-balancing_binary_search_tree)