**Sorting Fundamentals**
*Thu Oct 1*
[Link to Code](https://github.com/pomonacs622020fa/LectureCode/tree/master/SortingFundamentals)
# Transition to Prof Clark
- [Exam wrapper](https://cs.pomona.edu/classes/cs140/pdf/checkpoint-wrapper.pdf)
- We'll ask for feedback on using Sakai for exams next week
- We'll keep the same course structure for the rest of the semester
# Working with Git
~~~sh linenumbers
git clone https://github.com/pomonacs622020fa/LectureCode.git
git add some-file(s)
git status
git commit -am "some message"
git push origin master
~~~
I did not do this during class-time, but afterwards I added a `.gitignore` file to `LectureCode`.
~~~sh linenumbers
# I use a tool called gi: see https://docs.gitignore.io/
gi VisualStudioCode,java > .gitignore
git add .gitignore
git commit -am "Added a gitignore file for java and vscode."
~~~
One of your classmate gave a link to this [Unix Tutorial](https://faculty1.coloradocollege.edu/~sburns/UnixTutorial/index.html).
# Visual Studio Code
- Live Share extension
- Java extension
- Compiling and running from the command line
# Java
- Sortable objects must implement the [`Comparable`](https://docs.oracle.com/en/java/javase/14/docs/api/java.base/java/lang/Comparable.html) interface.
+ To implement the `Comparable` interface you must implement the `int compareTo(T that)` method
+ For example, calling `coolObject1.compareTo(coolObject2)` must return
* 0 if `coolObject1` and `coolObject2` are equal
* 1 if `coolObject1` is greater than `coolObject2`
* -1 if `coolObject1` is less than `coolObject2`
~~~java linenumbers
public class Student implements Comparable {
private String firstName;
private String lastName;
private int idNumber;
private static int ID_NUMBER = 0;
public Student(String firstName, String lastName) {
this.firstName = firstName;
this.lastName = lastName;
this.idNumber = ID_NUMBER;
ID_NUMBER++;
}
public String toString() {
return lastName + ", " + firstName + " (" + idNumber + ")";
}
@Override
public int compareTo(Student that) {
// Return 0 if they are equal
// Return 1 if this is greater than that
// Return -1 if this is less than that
return this.lastName.compareTo(that.lastName);
}
}
~~~
# Selection Sort
1. Divide the array into two parts: (left) a sorted subarray and (right) an unsorted subarray.
2. Repeat
1. Find the smallest element in the unsorted subarray.
2. Swap it with the leftmost unsorted element.
3. Shift subarray boundaries one to the right.
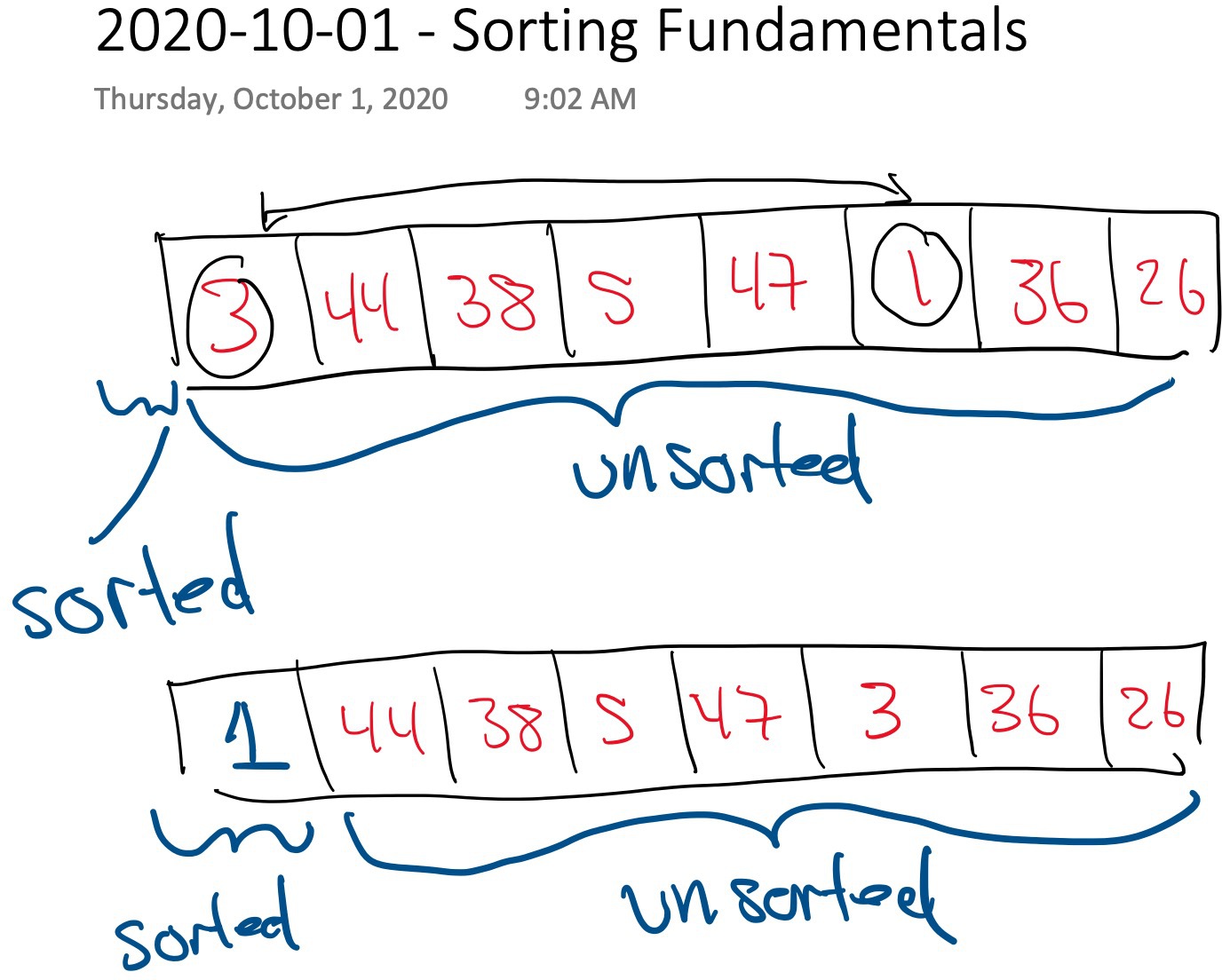
Questions:
- How many comparisons are made?
+ Answer: $(n-1) + (n-2) + ... + 2 + 1 \approx \frac{n^2}{2} = O(n^2)$
- How many exchanges are made?
+ Answer: $n-1 = O(n)$
- Is it in-place or not?
+ Answer: In-place
- Is it stable or not?
+ Answer: Not stable
Here is how you can use `SelectionSort` on *any* `ArrayList` of items that extend the `Comparable` interface.
~~~java
public static > void Sort(ArrayList list) {
// SelectionSort Code
}
~~~
Note: during class we encountered unexpected results when comparing [UUIDs](https://en.wikipedia.org/wiki/Universally_unique_identifier). Here is why: [java.util.UUID.compareTo() considered harmful](http://anuff.com/2011/04/javautiluuidcompareto-considered-harmful/).
You might also find this [ASCII table](https://www.rapidtables.com/code/text/ascii-table.html) useful, and this [discussion on UTF-8](https://utf8everywhere.org/).
# Insertion Sort
1. Divide the array into two parts: (left) a sorted subarray and (right) an unsorted subarray.
2. Repeat
1. Take the leftmost element of the unsorted subarray.
2. Insert this element into its correct position in the sorted subarray.
3. Shift subarray boundaries one to the right.
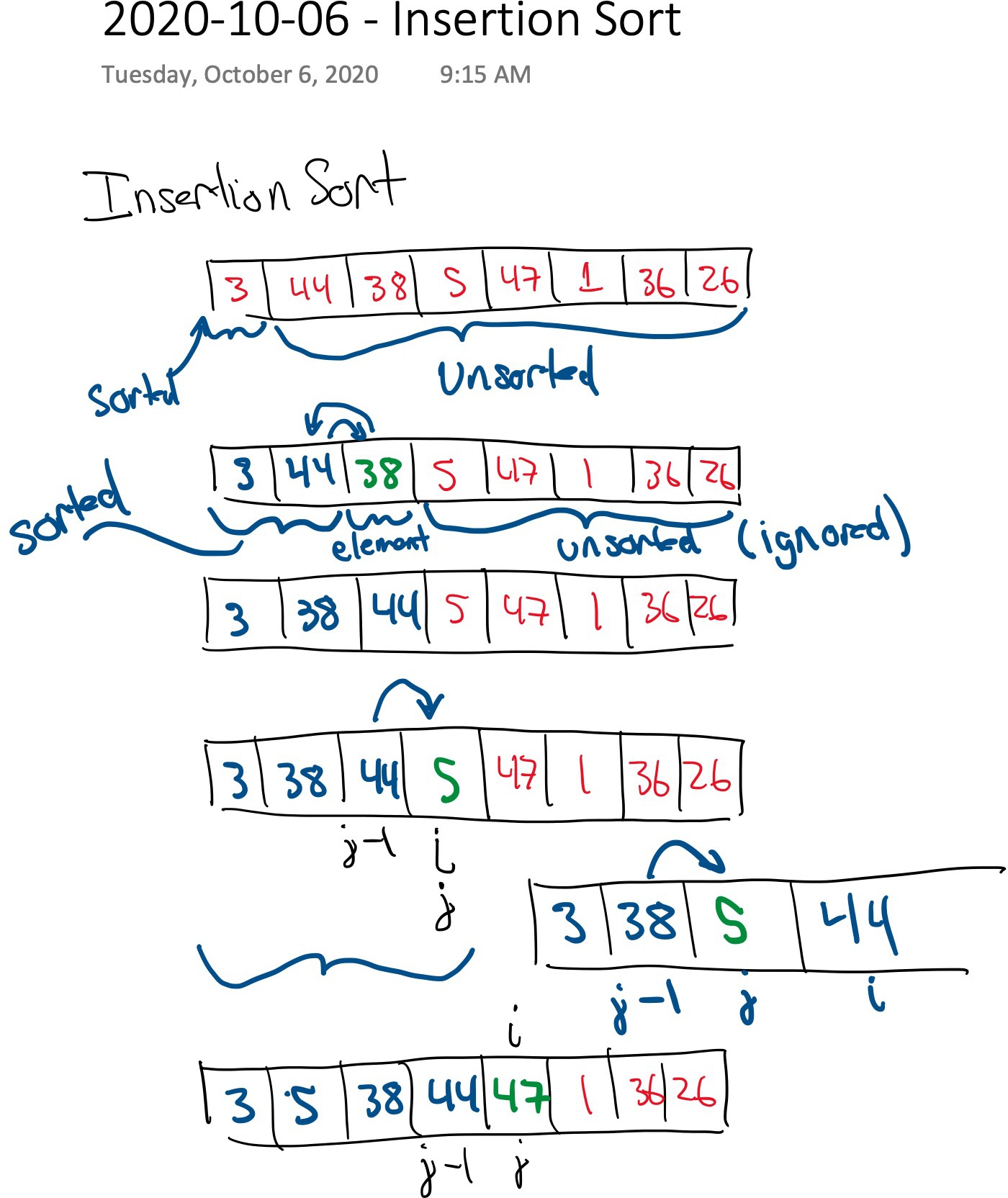
Questions:
- How many comparisons are made?
+ Answer:
* Worst-case: $1 + 2 + ... + (n-2) + (n-1) \approx \frac{n^2}{2} = O(n^2)$
* Best-case: $1 + 1 + ... + 1 + 1 = n-1 = O(n)$
- How many exchanges are made?
+ Answer:
* Worst-case: $1 + 2 + ... + (n-2) + (n-1) \approx \frac{n^2}{2} = O(n^2)$
* Best-case: $0 = O(1)$
- Is it in-place or not?
+ Answer: In-place
- Is it stable or not?
+ Answer: Stable
# Sorting Fundamentals
*What sorting algorithms do you know?*
- *Sorting*: arrange *n* items in **non-decreasing** order
- *Key*: property on which items are compared
- *In place*: use little or no extra memory
- *Stable*: items with duplicate keys maintain original order
# Stability Example
Below is an example of sorting stability.
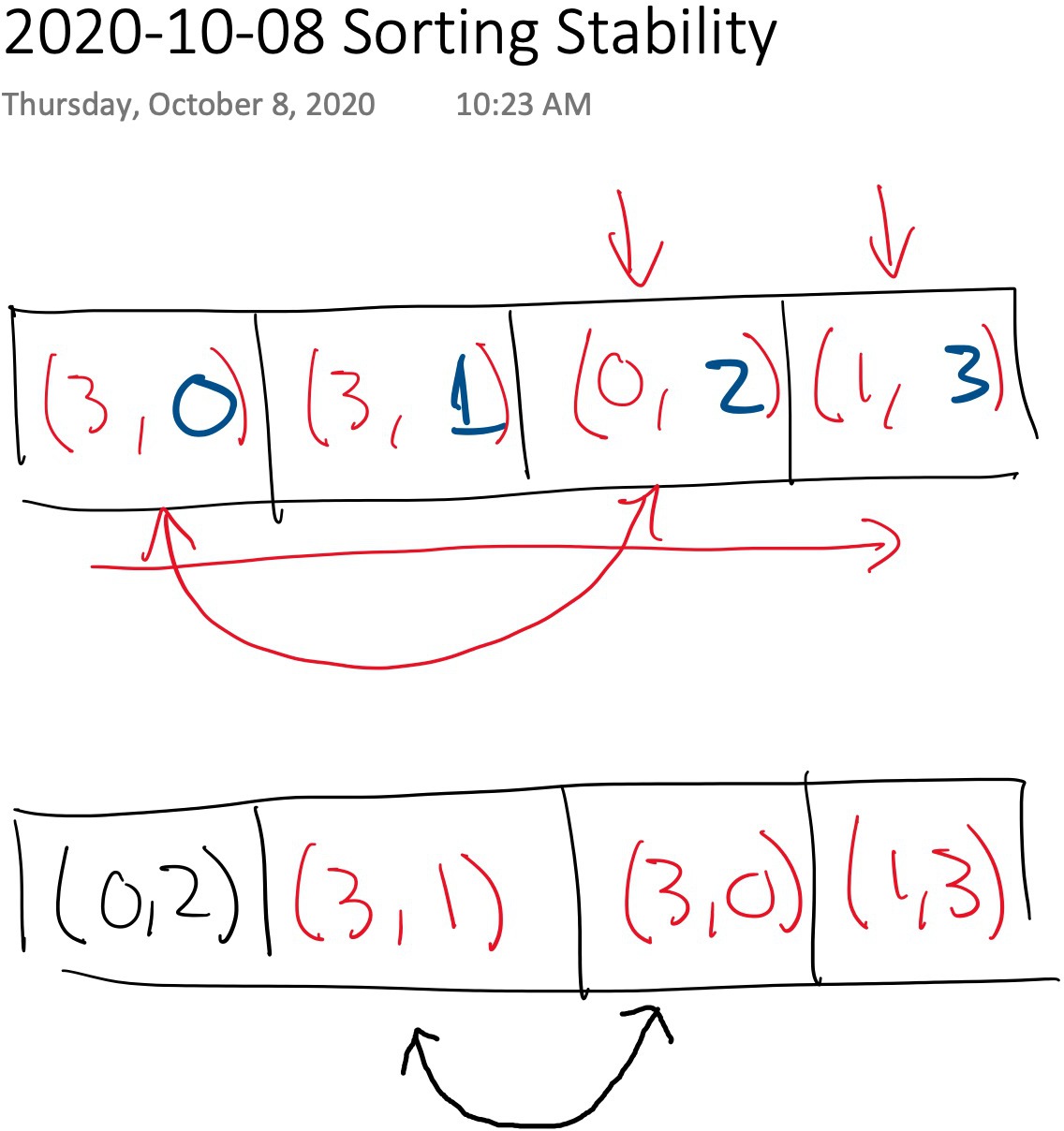
The above example shows what happens after one iteration of selection sort. In effect, the `(3, 0)` object is moved after the `(3, 1)` object, which violates stability.
**Why would you want a stable sort?** Consider what happens when you are using an application like Excel (or Google sheets). Imagine that the first column has students listed by first name and the second column has students listed by last name.
If you first sort by first name and then by last name, what would you like to happen?
- What happens if you are using a non-stable sorting algorithm?
- What happens if you are using a stable sorting algorithm?