Collision Detection

Game objects come in different shapes and sizes. The most important thing to remember is that the pixels making up a game character aren't all necessarily part of its collision boundary:

Often, a complex character is broken down into several simple shapes. Common candidates include:

• Points (lots of games used this)
• Line segments or rays
• Circles
• Axis-Aligned Bounding Boxes (a position and dimensions)
• Unaligned Bounding Boxes (a position, a direction, and dimensions)

But not all collision shapes are equivalent! It may be that some enemy should collide with the player but not with walls, or that the player should sometimes be able to swim through water and sometimes be able to walk on top of it. So collision shapes also tend to have some metadata: whether the object behind it is fixed in place or can move when bumped, whether it is solid or is just used to detect trigger conditions like the player entering a certain area. It's also worth noting that collision edges can have directions—sometimes you can jump up through something but not fall down through it.

A couple more important ideas from geometry for this week:

We'll work from these two interlocking assumptions to simplify our code:

1. Objects move slowly relative to their size and the size of obstacles.
2. Objects move instaneously from their position at one frame to their position in the next frame.

These mean that we can check whether collisions are happening after objects have moved, and just push the objects back a bit if they end up interpenetrating other objects at the end of the frame.

But these assumptions are not universally true! A projectile might move very quickly, and if the wall it's heading towards is narrower than the distance the projectile covers in a frame it will tunnel right through. Techniques like swept collision and smaller physics timesteps can mitigate these types of issues, but ultimately any numeric simulation will have instabilities and edge cases (analytic physics based on solving equations of motion can be perfectly precise, but prone instead to Zeno conditions and unpredictable execution time).

So at a high level our code will look like this:

1. Move objects
2. Detect collisions
3. Handle collisions

Moving objects, for now, will just be pos = pos + velocity. We'll fix our timestep to 60fps and set our velocity constants with respect to that frame rate.

We'll draw from a couple of good explanations for this section. The text here will be brief so please refer to those sources for detailed accounts.

There are lots of ways to determine whether particular combinations of shapes overlap. For example:

• A point touches a circle if the point is within radius of the circle's center
• Two circles touch if their centers are within the sums of their radii
• Two line segments intersect if we can find a point (x,y) that is on their corresponding lines and within the segments' start and end points
• A line \((p_1,p_2)\) touches a circle at \(c\) with radius \(r\) if the circle is not further than \(r\) from the line (check the dot product of the circle's center with the vector orthogonal to the line) and the dot product of the vector from \(p_1\) to \(c\) is between 0 and the length of the line (i.e., that the closest point on the circle to the line segment lies between the endpoints of the line segment)

We can extend the point and line checks to polygons by thinking of the polygon's edges as half-planes. A point is inside a polygon if it's inside every half-plane, and a line touches a polygon if either endpoint is inside or if the line segment intersects any edge. But what about polygon versus polygon collisions? We could check whether any edge of one intersects any edge of the other, or whether any vertex of one is inside the other, but this is a lot of work. Can we do better?

Yes! Intuitively, we can say that two polygons intersect if we can't draw a line that would separate them. So if one is inside the other then we certainly can't, or if they're touching then again we can't find an axis along which they could be split apart. Imagine that you have a flashlight and you can walk around the perimeter of the two polygons—if the light ever shines all the way through to the other side, there must be a gap between them. This claim is called the separating axis theorem.

How do we find a separating axis? We know that if a polygon is intersecting another polygon, it must be overlapping on every possible axis. But there are an infinite number of half-planes we could construct, so we certainly can't test every axis. It turns out that we only need to look at axes which are normal to the edges of one or the other polygon. Then, we find the interval that each polygon occupies along each axis (projecting each polygon's points onto the axis and taking the min and max of those projections), and if there's any axis where these intervals don't overlap we don't have a collision.

Let's make this concrete with an example of two rectangles.

Phew! Let's take a coding break. Put together a quick program where you control the movement of a square in four directions with the arrow keys.

The game you're making also needs a floor and ceiling (two wide stationary rectangles), two walls (tall stationary rectangles), and a platform (a flat, wide rectangle elevated above the floor). We won't introduce gravity yet (you'd fall right through!), but we will have physics: your character will accelerate at a constant rate depending on which directions are held down. If neither direction of an axis is held down, apply a braking acceleration in that axis. This could go in at the "determine player velocity" comment.

It might be a good idea to build your walls out of several rectangles, since some common collision bugs happen at the borders between rectangles. Here are my walls:

let walls = [
    // Top walls
    Wall::new(0,0,WIDTH/2,16),
    Wall::new(WIDTH/2,0,WIDTH/2,16),
    // Right walls
    Wall::new(WIDTH-16,0,16,HEIGHT/2),
    Wall::new(WIDTH-16,HEIGHT/2,16,HEIGHT/2),
    // ... same idea for left and bottom walls ...
    // Also a nice block in the middle
    Wall::new(WIDTH/2-16,HEIGHT/2-16,32,32)
];

Print out a distinct message when the square you control is touching a wall, floor, or platform. You could do this by (for example) adding a Type enum field to the Wall struct and another argument to new.

We often want to keep track of what has touched what, so we can do things like make Pong balls bounce or squish enemies in Mario. In order to avoid weird situations where handling one collision causes later objects to sometimes collide and sometimes not collide, we use collision detection to generate contacts which we later process. Another benefit of doing things this way is that we can let the computer repeat the same type of calculation (hopefully even the same exact code) over and over again, which makes better use of caches and pipelining.

A contact should store identifiers for the two colliding bodies (you might use usize indices into a Vec<Collider>) and the amount by which they're overlapping. Other information might be stored there as well.

In a real game, we would have more than a box and some walls. We can find which things are touching which other things by checking pairs of shapes:

let mut contacts = vec![];
for (i, body_i) in colliders.iter().enumerate() {
    for (j, body_j) in colliders.iter().enumerate().skip(i+1) {
        let displacement = match (body_i.shape, body_j.shape) {
            (Shape::Rect(ri), Shape::Rect(rj)) => ri.overlap(rj),
            (Shape::Circle(_), Shape::Point) => point_circle_disp(body_j, body_i),
            (Shape::Point, Shape::Circle(_)) => point_circle_disp(body_i, body_j),
            //... a dozen more cases...
            (Shape::Poly(_), Shape::Poly(_)) => sat(body_i, body_j)
        };
        if let Some(disp) = displacement {
            contacts.push(Contact(i, j, disp));
        }
    }
}

Note that we use skip to avoid half of the possible collision checks. Note also that this kind of stinks due to all those match statements! We could shove the logic for picking the right collision function into the Shape enum using double dispatch (e.g. if self is a point, call other.collide_point(self), which itself matches on self (previously known as other) to select the right function), and while that would fix the problem for human readers it doesn't change much for the computer. If we decided to use virtual functions (in Rust world, trait objects) we'd have to pay even greater costs.

Another approach is to group shapes together. Instead of one loop over a collection of every shape, we'll have one collection per shape type and check each against the others.

let mut contacts = vec![];
for (i, pi) in points.iter().enumerate() {
    for (j, cj) in circles.iter().enumerate() {
        if let Some(disp) = point_circle_disp(pi, cj) {
            // Whoops, Contact now tracks the collections the contact bodies came from as well.
            // Instead of body indices we may prefer to track game object IDs and forget the specific collider shapes involved.
            contacts.push(Contact(&points, i, &circles, j, disp));
        }
    }
}
for (i, ci) in circles.iter().enumerate() {
    for (j, cj) in circles.iter().enumerate().skip(i+1) {
        // same deal here, circle vs circle
    }
}
// More loops like those

Is it more code? Undoubtedly! But it's much more predictable and less branchy.

But we have another way to both reduce branching and improve legibility: only support collision checking between axis-aligned rectangles—AABBs. The lesson here is to structure your code using all the knowledge you have at hand, and not make the computer do extra work because you haven't prepared the data the way it likes (e.g. demanding more flexibility than you actually make use of); or even better, to take on reasonable design restrictions to avoid the need for flexibility at all!

In the simple case of one player rectangle and some number of walls, something like this could work:

const COLLISION_STEPS: usize = 3;
for _step in 0..COLLISION_STEPS {
    // Gathering contacts for the player against each wall
    let mut touching_rects: Vec<(usize,Vec2i)> = state
        .walls
        .iter()
        .enumerate()
        .filter_map(|(ri,r)| {
            r.overlap(Rect {
                pos: player_pos,
                sz: PLAYER_SZ,
            }).map(|o| (ri,o))
        })
        .collect();
    // Sort by magnitude
    touching_rects.sort_by_key(|(_ri,o)| -o.sq_mag());
    if touching_rects.is_empty() { break; }
    // Resolve collisions
    // ...
}

If we had multiple moving objects, we'd want to loop within each collision step to gather all contacts between pairs of objects and then resolve all contacts (we saw how iterating over pairs of objects looked earlier). We'd probably have a "resolved" flag and this-frame displacement vector for each moving object.

Most techniques for broad phase collision detection use some form of spatial partitioning datastructure, where objects are somehow binned according to their relative locations (or sometimes absolute locations, as in locality sensitive hashing or by recording objects' memberships in a coarse grid superimposed on the game world).

One particularly common technique is based around tree partitioning (e.g. BSP trees, quadtrees, octrees). In these approaches, we represent space as a tree (with some branching factor) whose nodes hold buckets of objects of some maximum capacity (a non-leaf node's objects will be those that overlap two or more of its child nodes). Because we know the tree splits space according to some rule, we can find the buckets and therefore the objects nearest to a particular point in logarithmic time, rather than by iterating through the whole list of objects. As objects move we can rebalance the tree, or we can just recreate the tree from scratch every so often. Besides querying for the objects within a volume, we can use the tree structure to guide our collision detection: to generate contacts for a node we generate contacts within its objects and between its objects and those of its children. We still can't avoid \(O(n^2)\) collision detection, but at least we can keep \(n\) very low in most cases.

Spatial partitioning data structures are also really useful to determine what we need to actually draw on screen, especially in 3D: we shouldn't spend valuable time drawing objects that are off-screen or behind other opaque objects!

If we already know that objects in cells of unrelated spatial partitions won't collide with each other, then there's no reason to process all the objects in the first cell before moving on to those of the second. So we can process all the cells in parallel, taking advantage of our preponderance of CPU cores to generate contacts even faster. In Rust, the rayon crate implements a work-stealing queue which can be a good fit for this kind of data parallelism, especially since less-populous tree nodes will take less time to process than more densely populated ones.

Part of why we set up contact generation as a distinct step from collision resolution is to enable this kind of order-independent and concurrent processing. Especially since the era of the PlayStation 3, taking full advantage of data parallelism has been vital for achieving the performance targets set by recent trends in game design.

There's a really solid collision detection crate for Rust called parry, so you can totally use that; another good option is ncollide.

Even if it's moving very slowly, a video game object that bumps into a wall is most likely, at the moment it bumps into the wall, actually partially inside of that wall. Because of our assumption that objects are moving slowly, we can further assume we can always find a good displacement that would cause the collision to cease happening. This is often called the minimum translation vector since it's the least difficult way to move the objects out of interpenetration. In this example it's the blue arrow:

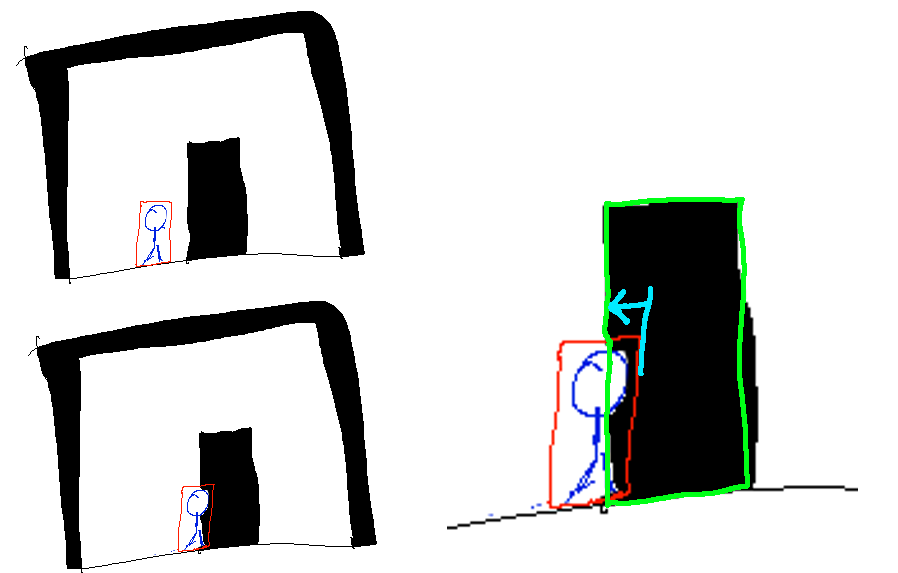
In this case, the whole MTV gets assigned to the moving object rather than, say, half to the object and half to the wall. If both parties in the collision were movable, then we might displace each by half (in opposite directions) or by share the vector based on the relative momentum of the two objects.

No matter how you decide on the displacements, if you ever displace opposite to the character's velocity in a component, you should probably force that velocity to reflect the displacement somehow (for example, if a character bumps the ceiling its y velocity should be set to 0).

Sometimes, we might be simultaneously experiencing two collisions, and they have contradictory resolutions. Imagine the following scene, with a character moving upwards and rightwards at a 45 degree angle. They'll end up inside of both the wall and the closed door:

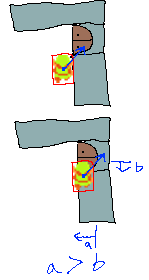
Collision against the closed door is mostly on the character's top edge, while collision against the wall is mostly on the character's right edge. So what do we do? If we process horizontal collisions first, then vertical ones, we'll bump the player out to the left and then bump them downwards—even though they're not colliding with the door after restitution! If we just picked the bigger of the restitutions, then if we were up in the top-right corner we'd find ourselves starting to move through either the door or the top wall. I've only shown the minimal component of the MTVs \(a\) and \(b\) here, but remember those are both vectors pointing roughly from the invading object's leading corner or edge towards the point where it entered the wall/door. (Our displacement vector from SAT before wasn't yet an MTV—we hadn't yet picked the best direction to separate the objects. Luckily, we can compare the relative positions of the objects' centers to obtain the right signs to put on the components of our displacement vector. You can do this in e.g. rect_displacement or when computing the collision response.)

There are a variety of tricks one can use to mitigate this type of bug in different settings, and the true answer will involve solving systems of linear equations to find the optimal impulses that will displace the objects correctly, then updating the positions using a differential equation solver. For now, in the 2D, AABB setting, we'll solve it by asking which collision happened first and trying to restitute our way out of that one.

In the example above, the wall collision happens before the door collision since in some sense we're already touching the wall. At any rate, more of the "mass" of the contact is in the wall than in the door, so the wall-player displacement is larger than the door-player displacement (even though both are their contacts' respective MTVs). So we can sort the contacts by decreasing magnitude (or squared magnitude) of their MTVs, and process the bigger contacts first. Note that we've thrown all the contacts into one big list above (or e.g. one per broad-phase partition unit), so if we can continue processing big lists of contacts in uniform ways our instruction cache, data cache, and load predictor will thank us. If, on the other hand, we need to handle different sorts of contacts differently, we should either separate them out or change the processing so that we can handle them uniformly.

Sorting the contacts tells us which ones to handle first, but it doesn't on its own fix the double-restitution issue. For that, we have two options after we move the objects out of collision when handling a particular contact:

1. Record, for each object, how much it has been restituted already; we can do this by altering the MTV of later contacts involving this object after the collision response is applied, or by storing an auxiliary data structure.
   • If this change to the MTV causes it to cross zero in either dimension, then we know the objects aren't touching anymore! If it exactly hits zero then they're perfectly lined up.
2. Right before we handle a contact, check to be sure the objects involved are still actually touching and if so use the new MTV. This does extra work, so beware!

Collision detection always accumulates edge cases and tricks to make it feel better. Here's an example of simple player-vs-walls collision restitution. You'll want to generalize it for your game—introduce some nested loop over pairs of objects to generate contacts, and then a loop through those contacts to perform restitution.

let mut disps = Vec2i{x:0,y:0};
const COLLISION_STEPS: usize = 3;
for _step in 0..COLLISION_STEPS {
    // ... gather contacts as above...
    // Now restitute contacts:
    let mut resolved = false;
    for (ri,mut ov) in touching_rects.iter() {
        // Touching but not overlapping
        if ov.x == 0 || ov.y == 0 {
            resolved = true;
            // Maybe track "I'm touching it on this side or that side"
            break;
        }
        // figure out which components of o should be negated---is player left or above the wall?
        // This is needlessly specialized.
        // In a real game this would be "is thing 1 left or above thing 2"?
        if state.player_pos.x + PLAYER_SZ.x/2 < state.walls[*ri].midpoint().x {
            ov.x = -ov.x;
        }
        if state.player_pos.y + PLAYER_SZ.y/2 < state.walls[*ri].midpoint().y {
            ov.y = -ov.y;
        }
        // Is this more of a horizontal collision... (and we are allowed to displace horizontally)
        if ov.x.abs() <= ov.y.abs() && ov.x.signum() != -disps.x.signum() {
            // Record that we moved by o.x, to avoid contradictory moves later
            disps.x += o.x;
            // Actually move player pos
            state.player_pos.x += o.x;
            // Mark collision for the player as resolved.
            resolved = true;
            break;
            // or is it more of a vertical collision (and we are allowed to displace vertically)
        } else if ov.y.abs() <= ov.x.abs() && ov.y.signum() != -disps.y.signum() {
            disps.y += o.y;
            state.player_pos.y += o.y;
            resolved = true;
            break;
        } else {
            // otherwise, we can't actually handle this displacement because we had a contradictory
            // displacement earlier in the frame.
        }
    }
    // Couldn't resolve collision, player must be squashed or trapped (e.g. by a moving platform)
    if !resolved {
        // In your game, this might mean killing the player character or moving them somewhere else
        squished = true;
    }
}

No matter which approach we use here, it's always possible that restituting one collision will cause another one to happen. This is unavoidable if we're just looking at one contact at a time rather than solving the entire system of equations simultaneously. But that's a lot of heavy machinery to bring in right now, and we can avoid the need for it with careful game design for now. Also note that if our character from the example above were represented as just four corner pixels, we could write more specialized code: If the northeast and southeast pixels are both colliding, but the northwest and southwest ones are not, just restitute westward; If only the northeast pixel is colliding, we could just restitute downward; and so on.

Note that not all collision contacts will be important for restitution. You might consider having two classes of colliders: solid objects and trigger volumes. It's vital to generate contacts against triggers, but they shouldn't cause the object touching them to move around. It's up to you whether to combine both types of collision checks into one phase, or whether to process collisions with triggers separately from collisions with regular bodies.

Whatever techniques you use, at this point you have a world with (hopefully) no interpenetrations and rich information about which objects actually touched which other objects in the scene. It's time to make a videogame!

It is worth noting that this is starting to look like "physics", so it might be worth exploring rapier, a physics engine for Rust games. Physics aren't always the best fit for 2D games (e.g., a top-down, tile-oriented game like The Legend of Zelda might feel awkward with proper physics), but it is possible to use colliders without using rigid body physics. Something like rapier or nphysics will add a lot of complexity, but it may be worth it if it's too hard to think through edge cases in collision.

I didn't talk about it above because we won't be needing it where we're going. I won't get too into it now, but consider that as programmers we want to write general-purpose code that solves the most general problems we need to solve. Asking one object if it's touching a second object is not a very general case in collision detection, but an extremely special case. Really, we have a big soup of things that may or may not be touching, and we need to output data describing what's touching what. It doesn't hurt that this approach doesn't pay for virtual function calls, pointer and reference chasing, and a host of other overheads in pursuit of flexibility along an axis of generality we don't really need (how many fundamentally different collision checkers are we really going to have?).

As we hinted before, we want some tiles to be solid and others to be… not… solid. The simplest type of collision we can implement was used pretty often in old computer role-playing games, and still appears in specialized game engines like Bitsy.

Naively, we might expect that we'd handle collision with a tilemap by treating each tile as a little square, and then check collisions between those squares and the character. But nearly all tiles are not colliding with anything, and they can't collide with each other, so this representation is wasteful. Moreover, tiles are on a uniform grid so there's no need to store per-tile location or size information. It's therefore a good idea to have a specialized collision detection function to determine if a sprite is colliding with something in a tilemap.

It's also important to note that even though tiles are square, the underlying terrain might be shaped differently. This could be mostly graphical—for example, the squareness of the dirt and grass tiles is concealed in the second screenshot above, and moving upwards it blends into rocks, trees, and sunlight with the forest canopy in the distance. It could also be physical. In the image below, we see Mario sliding down a slope. While the slope tile visually is a square with a black diagonal line through it and green underneath the line, the game is coded so that Mario's vertical position while standing on a slope is a function of his horizontal displacement within the slope tile. When Mario is on the left edge of the tile, he is at the slope's minimum, when halfway across he is at the midpoint, and then he's on the right edge he's at the slope's maximum. If we wanted to support this we'd add new flags or numeric properties to our Tile struct above to indicate the tile's "real" shape.

How do we find out what tiles a character is standing on or touching? Collision detection with a tilemap can be extremely efficient. First, recall that a tilemap is a grid of tiles positioned somewhere in space. Since we can convert from world coordinates to tile coordinates by a subtraction and a division, we can find out where the sprite is on the tilemap. We could, for example, look at the sprite's four corners, or its four corners plus the top of its head and center of its feet. If we know those positions, we can find the corresponding tiles and check their collision properties to determine if the sprite is touching something solid on its respective sides. If so, we can prevent the sprite's movement—as if the sprite were colliding with a square positioned where the tile is, or even handle different collisions specially. For example, we could use the foot's contacted tile and horizontal location on the tile grid to determine the character's new y position, or we could move the sprite to the nearest tile boundary if its top or right edge tiles are overlapping something solid.