2D Graphics
[ ]What is a framebuffer?[ ]How are 2D graphics stored on a computer in linear memory?[ ]Can I easily convert between linear memory indices and 2D coordinates \((x,y)\)?[ ]Why is it OK to pass a reference to aVec<P>into a function expecting&mut [P]?[ ]How do we update a texture on the GPU?[ ]How much time we do we have every frame for input handling, simulation, and drawing?[ ]What is bitblit and why is it useful?- In other words, when might we not want to draw an entire image at once?
Framebuffer Graphics
Time for a quick story. The computer screen you're looking at is a bunch of photons flying at your face from a backlight which is color-filtered through a number of layers of electrosensitive liquid crystals (or possibly it's an organic LED matrix and the photons are excited by the dielectric effect). Before that, though, it's an incredibly fast sequence of images sent over a wire as a stream of color values grouped into pixels. Each pixel is probably a red/green/blue triple, grouped into rows with the rows grouped into grids called frames. Each frame lasts a fraction of a second, and by creating slightly different frames extremely rapidly the computer tricks your brain into seeing the illusion of motion.
On your computer, a complex interaction of software (compositors) and hardware (graphics adapters) works to assemble a bunch of programs' output into a coherent image efficiently. We're going to look back to a simpler time, a time before "multi-tasking", back to when it was routine for a program to take over the graphics card completely and blast a grid of pixels directly from memory (our "frame buffer") to the screen, with a blazing fast processor running at literally dozens of MHz capable of rewriting a whole 320x240 pixels thirty times per second.
We're going to implement a software renderer for framebuffer graphics.
What is a picture?
On a computer, we can represent pictures lots of different ways:
- A grid of RGB pixels
- How many bits for each color component for each pixel?
- Other color spaces: LAB, HSV, CMYK, …
- A collection of graphical primitives
- A small background grid of "tiles" (identifiers representing pre-set 8x8 pixel graphics) and up to 64 "sprites", each of which can be assigned a pre-set 8x8 graphic but moved around freely on the screen
- A collection of vertices, a list indicating which of them form triangles, and a program for coloring in bits of triangles
- A superposition of intensity waveforms for each color channel
- …
In this unit we'll use the first representation as our foundation and build from there. There are five important things to know about a framebuffer (the region of memory holding a frame):
- How wide is it?
- How tall is it?
- How many color components do we need per pixel?
- How many bits do we need per color component and what type should we use?
- Are the colors all interleaved, or do we have a separate single-color image for each color component?
Memory on a computer is essentially linear, so we also need a way to map this 3D tensor (\(W \times H \times C\) or \(C \times W \times H\)) to a 1D array. To do this, we take our grid rows (starting from the top) and lay them out one after another in linear memory:
// Instead of this for an RGB888 image... let mut fb = [[[0_u8; 3]; WIDTH]; HEIGHT]; // Try this: let mut fb = [0_u8; WIDTH*HEIGHT*3]; // Or this if you want it on the heap: let mut fb = vec![0_u8; WIDTH*HEIGHT*3];
It's not wrong per se to use the first representation, but we can only use it effectively if we know the image size in advance. This is because we know those arrays are laid out contiguously in memory. If we used this instead:
// Definitely don't do this let mut fb = vec![vec![vec![0_u8; 3]; WIDTH]; HEIGHT];
Each of the WIDTH*HEIGHT Vecs has its own heap allocation (and its own capacity and length fields!) so this is not only wasteful, but highly non-local. Pointers to pointers everywhere!
As an aside, you might ask "why do we go by rows outside and not by columns?" Well, it's arbitrary but it's a common convention. Framebuffers are usually wider than they are tall so it helps some with effective cache utilization, but there's no deep reason.
Now that we have a linear framebuffer, what can we do with it? In particular, how can we address a particular (x,y) coordinate in that linear array—say, to turn it red?
fb[y*WIDTH*3+x*3+0] = 255; fb[y*WIDTH*3+x*3+1] = 0; fb[y*WIDTH*3+x*3+2] = 0;
what
There's a lot of multiplications going on here. Remember when we said we wanted to lay out each row one after the other? The consequence of that is that each additional y increment has to jump us forward in the array by one row—and since each pixel itself has three elements (red value, green value, and blue value) we need to jump ahead by y*WIDTH many rows, each of which has 3 elements. That gives us our pitch or vertical stride of WIDTH*3.
After we get to the right row for the y component, we're still not done. Now we need to account for the x component, which we multiply by our component count (3 again) or horizontal stride.
At this point we're in the right pixel, and can start writing values. If a pixel is made of three colors, we need to make three writes: one to the red value (start + 0), one to the green (start + 1), and one to the blue (start + 2). This is assuming what's called an rgb888 image, but other pixel formats are possible, some of which have different horizontal strides: rgba8888, rgba32, rgb565, rgb332, argb32, and more have been or are still used by some software and hardware (the a stands for "alpha", which we're going to handle before it gets to the framebuffer).
It's a good idea to pack up your indexing logic (converting from x, y, stride, and pitch to an index, or vice versa) into some helper functions or even a nice struct:
pub struct FramebufferRGB888 { width:usize, height:usize, data:Vec<u8> // or Box<[u8]> is slightly cheaper. Vec<RGB888> would be okay too. } pub struct RGB888(pub u8,pub u8,pub u8); impl FramebufferRGB888 { pub fn new(width:usize, height:usize) -> Self { //... } #[inline(always)] pub fn get(&self, x:usize, y:usize) -> Color { //... } #[inline(always)] pub fn set(&mut self, x:usize, y:usize, c:Color) { //... } }
That said, for this to be really useful you'll also want to implement some niceties like iter_mut, chunks_exact, and friends. So until you're more familiar with what Rust has to offer we'll get by with just these two helpers and use Vec<u8> or Vec<RGB888> everywhere:
// If you're using Vec<Color> instead of Vec<u8> you can skip stride #[inline(always)] fn to_index(x:usize,y:usize,w:usize,stride:usize) -> usize { y*w*stride+x*stride } // That would save you a division and multiplication here too, which would be nice #[inline(always)] fn to_pos(index:usize, w:usize, stride:usize) -> (usize, usize) { let pitch = w * stride; let y = index / pitch; let x = (index - y*pitch) / stride; (x,y) }
Phew. That was a lot, and we didn't even talk about the bitwise operations you'll need for formats that don't use exactly one byte (or float) per pixel. Let's draw something.
Clearing and Drawing
First let's do our background color. I'll use a P struct now for RGBA8888 pixels.
#[derive(PartialEq,Eq,Clone,Copy)] struct P(u8,u8,u8,u8); let mut fb = vec![P(0,0,0,0); WIDTH*HEIGHT]; // A soft black-ish color with blue tint, full alpha let bg = P(32,32,64,255);
We could certainly do this:
// Always go row first if your images are row-major for y in 0..HEIGHT { for x in 0..WIDTH { // Note stride is 1 now so this version of to_index omits it fb[to_index(x,y,WIDTH)] = bg; } }
But this is tighter and could optimize better:
fn clear(fb:&mut [P], bg:P) { for px in fb.iter_mut() { *px = bg; } }
Even better:
fn clear(fb:&mut [P], bg:P) { fb.fill(bg); }
Now that we have our background set, we can finally draw something.
A nice horizontal line will be a good start. We'll do it two ways.
fn line(fb: &mut [P], x0: usize, x1: usize, y: usize, c: P) { for x in x0..x1 { fb[to_index(x,y)] = c; } }
But each indexing access we do means a bounds check which we'd rather avoid.
fn line(fb: &mut [P], x0: usize, x1: usize, y: usize, c: P) { assert!(y < HEIGHT); assert!(x0 <= x1); assert!(x1 < WIDTH); fb[(y*WIDTH+x0)..(y*WIDTH+x1)].fill(c); }
This version only needs to check the lower and upper bounds of the range to be modified, while the first version needs to check every single position in the line. The asserts are there just in case.
Do you think we should draw the line up to x1, or to x1+1?
Drawing in a Program
Let's put this together into a real program. We'll draw a bunch of pretty lines.
[package] name = "line-drawing" version = "0.1.0" authors = ["Joseph C. Osborn <joseph.osborn@pomona.edu>"] edition = "2021" [dependencies] vulkano = "0.27.1" vulkano-shaders = "0.27.1" winit = "0.25" vulkano-win = "0.27.1" png = "0.17"
There are four key changes here. Find the places in code where these changes were made:
- We've changed our texture from an
ImmutableImageloaded from disk into aStorageImage. - We set up both a CPU-side framebuffer (
fb2d) and a GPU-sideCpuAccessibleBuffer. Each frame, that buffer will be copied into the texture. - Every frame, before issuing our draw command we need to copy
fb2dinto the GPU-side buffer. We also need to wait for the GPU to finish using that GPU-side buffer (it would be Bad if we tried to change the buffer while the GPU was copying from it—luckily, Vulkano turns this into a runtime error). - We added a little bit of drawing code to draw lines at different places.
// Based on the Vulkano triangle example. // Triangle example Copyright (c) 2016 The vulkano developers // Licensed under the Apache License, Version 2.0 // <LICENSE-APACHE or // https://www.apache.org/licenses/LICENSE-2.0> or the MIT // license <LICENSE-MIT or https://opensource.org/licenses/MIT>, // at your option. All files in the project carrying such // notice may not be copied, modified, or distributed except // according to those terms. use vulkano::image::ImageCreateFlags; use std::sync::Arc; use vulkano::buffer::{BufferUsage, CpuAccessibleBuffer, TypedBufferAccess}; use vulkano::command_buffer::{AutoCommandBufferBuilder, CommandBufferUsage, SubpassContents}; use vulkano::descriptor_set::PersistentDescriptorSet; use vulkano::device::physical::{PhysicalDevice, PhysicalDeviceType}; use vulkano::device::{Device, DeviceExtensions, Features}; use vulkano::format::Format; use vulkano::image::{ view::ImageView, ImageAccess, ImageDimensions, ImageUsage, SwapchainImage, StorageImage }; use vulkano::instance::Instance; use vulkano::pipeline::graphics::input_assembly::InputAssemblyState; use vulkano::pipeline::graphics::vertex_input::BuffersDefinition; use vulkano::pipeline::graphics::viewport::{Viewport, ViewportState}; use vulkano::pipeline::{GraphicsPipeline, PipelineBindPoint, Pipeline}; use vulkano::render_pass::{Framebuffer, RenderPass, Subpass}; use vulkano::sampler::{Filter, MipmapMode, Sampler, SamplerAddressMode}; use vulkano::swapchain::{self, AcquireError, Swapchain, SwapchainCreationError}; use vulkano::sync::{self, FlushError, GpuFuture}; use vulkano::Version; use vulkano_win::VkSurfaceBuild; use winit::event::{Event, WindowEvent}; use winit::event_loop::{ControlFlow, EventLoop}; use winit::window::{Window, WindowBuilder}; // We'll make our Color type an RGBA8888 pixel. type Color = (u8,u8,u8,u8); const WIDTH: usize = 320; const HEIGHT: usize = 240; // Here's what clear looks like, though we won't use it #[allow(dead_code)] fn clear(fb:&mut [Color], c:Color) { fb.fill(c); } #[allow(dead_code)] fn line(fb: &mut [Color], x0: usize, x1: usize, y: usize, c: Color) { assert!(y < HEIGHT); assert!(x0 <= x1); assert!(x1 < WIDTH); fb[y*WIDTH+x0 .. (y*WIDTH+x1)].fill(c); } fn main() { let required_extensions = vulkano_win::required_extensions(); let instance = Instance::new(None, Version::V1_1, &required_extensions, None).unwrap(); let event_loop = EventLoop::new(); let surface = WindowBuilder::new() .build_vk_surface(&event_loop, instance.clone()) .unwrap(); let device_extensions = DeviceExtensions { khr_swapchain: true, ..DeviceExtensions::none() }; let (physical_device, queue_family) = PhysicalDevice::enumerate(&instance) .filter(|&p| { p.supported_extensions().is_superset_of(&device_extensions) }) .filter_map(|p| { p.queue_families() .find(|&q| { q.supports_graphics() && surface.is_supported(q).unwrap_or(false) }) .map(|q| (p, q)) }) .min_by_key(|(p, _)| { match p.properties().device_type { PhysicalDeviceType::DiscreteGpu => 0, PhysicalDeviceType::IntegratedGpu => 1, PhysicalDeviceType::VirtualGpu => 2, PhysicalDeviceType::Cpu => 3, PhysicalDeviceType::Other => 4, } }) .unwrap(); let (device, mut queues) = Device::new( physical_device, &Features::none(), &physical_device .required_extensions() .union(&device_extensions), [(queue_family, 0.5)].iter().cloned(), ) .unwrap(); let queue = queues.next().unwrap(); let (mut swapchain, images) = { let caps = surface.capabilities(physical_device).unwrap(); let composite_alpha = caps.supported_composite_alpha.iter().next().unwrap(); let format = caps.supported_formats[0].0; let dimensions: [u32; 2] = surface.window().inner_size().into(); Swapchain::start(device.clone(), surface.clone()) .num_images(caps.min_image_count) .format(format) .dimensions(dimensions) .usage(ImageUsage::color_attachment()) .sharing_mode(&queue) .composite_alpha(composite_alpha) .build() .unwrap() }; // We now create a buffer that will store the shape of our triangle. #[derive(Default, Debug, Clone)] struct Vertex { position: [f32; 2], uv: [f32;2] } vulkano::impl_vertex!(Vertex, position, uv); let vertex_buffer = CpuAccessibleBuffer::from_iter( device.clone(), BufferUsage::all(), false, [ Vertex { position: [-1.0, -1.0], uv: [0.0, 0.0] }, Vertex { position: [3.0, -1.0], uv: [2.0, 0.0] }, Vertex { position: [-1.0, 3.0], uv: [0.0, 2.0] }, ] .iter() .cloned(), ) .unwrap(); mod vs { vulkano_shaders::shader! { ty: "vertex", src: " #version 450 layout(location = 0) in vec2 position; layout(location = 1) in vec2 uv; layout(location = 0) out vec2 out_uv; void main() { gl_Position = vec4(position, 0.0, 1.0); out_uv = uv; } " } } mod fs { vulkano_shaders::shader! { ty: "fragment", src: " #version 450 layout(set = 0, binding = 0) uniform sampler2D tex; layout(location = 0) in vec2 uv; layout(location = 0) out vec4 f_color; void main() { f_color = texture(tex, uv); } " } } let vs = vs::load(device.clone()).unwrap(); let fs = fs::load(device.clone()).unwrap(); // Here's our (2D drawing) framebuffer. let mut fb2d = vec![(128,64,64,255); WIDTH*HEIGHT]; // We'll work on it locally, and copy it to a GPU buffer every frame. // Then on the GPU, we'll copy it into an Image. let fb2d_buffer = CpuAccessibleBuffer::from_iter( device.clone(), BufferUsage::transfer_source(), false, (0..WIDTH*HEIGHT).map(|_| (255_u8,0_u8,0_u8,0_u8)) ).unwrap(); // Let's set up the Image we'll copy into: let dimensions = ImageDimensions::Dim2d { width: WIDTH as u32, height: HEIGHT as u32, array_layers: 1, }; let fb2d_image = StorageImage::with_usage( device.clone(), dimensions, Format::R8G8B8A8_UNORM, ImageUsage { // This part is key! transfer_destination: true, sampled: true, storage: true, transfer_source: false, color_attachment: false, depth_stencil_attachment: false, transient_attachment: false, input_attachment: false, }, ImageCreateFlags::default(), std::iter::once(queue_family) ).unwrap(); // Get a view on it to use as a texture: let fb2d_texture = ImageView::new(fb2d_image.clone()).unwrap(); let fb2d_sampler = Sampler::new( device.clone(), Filter::Linear, Filter::Linear, MipmapMode::Nearest, SamplerAddressMode::Repeat, SamplerAddressMode::Repeat, SamplerAddressMode::Repeat, 0.0, 1.0, 0.0, 0.0, ) .unwrap(); let render_pass = vulkano::single_pass_renderpass!( device.clone(), attachments: { color: { // Pro move: We're going to cover the screen completely. Trust us! load: DontCare, store: Store, format: swapchain.format(), samples: 1, } }, pass: { color: [color], depth_stencil: {} } ) .unwrap(); let pipeline = GraphicsPipeline::start() .vertex_input_state(BuffersDefinition::new().vertex::<Vertex>()) .vertex_shader(vs.entry_point("main").unwrap(), ()) .input_assembly_state(InputAssemblyState::new()) .viewport_state(ViewportState::viewport_dynamic_scissor_irrelevant()) .fragment_shader(fs.entry_point("main").unwrap(), ()) .render_pass(Subpass::from(render_pass.clone(), 0).unwrap()) .build(device.clone()) .unwrap(); let layout = pipeline.layout().descriptor_set_layouts().get(0).unwrap(); let mut set_builder = PersistentDescriptorSet::start(layout.clone()); set_builder .add_sampled_image(fb2d_texture, fb2d_sampler) .unwrap(); let set = set_builder.build().unwrap(); let mut viewport = Viewport { origin: [0.0, 0.0], dimensions: [0.0, 0.0], depth_range: 0.0..1.0, }; let mut framebuffers = window_size_dependent_setup(&images, render_pass.clone(), &mut viewport); let mut recreate_swapchain = false; let mut previous_frame_end = Some(sync::now(device.clone()).boxed()); let mut y = 0; event_loop.run(move |event, _, control_flow| { match event { Event::WindowEvent { event: WindowEvent::CloseRequested, .. } => { *control_flow = ControlFlow::Exit; } Event::WindowEvent { event: WindowEvent::Resized(_), .. } => { recreate_swapchain = true; }, Event::MainEventsCleared => { { // We need to synchronize here to send new data to the GPU. // We can't send the new framebuffer until the previous frame is done being drawn. // Dropping the future will block until it's done. if let Some(mut fut) = previous_frame_end.take() { fut.cleanup_finished(); } } // We can update our local framebuffer here: y = (y + 7) % HEIGHT; line(&mut fb2d, WIDTH/4, WIDTH-WIDTH/4, y, (255-(y as u8 % 255), 0, y as u8 % 255, 255)); // Now we can copy into our buffer. { let writable_fb = &mut *fb2d_buffer.write().unwrap(); writable_fb.copy_from_slice(&fb2d); } if recreate_swapchain { let dimensions: [u32; 2] = surface.window().inner_size().into(); let (new_swapchain, new_images) = match swapchain.recreate().dimensions(dimensions).build() { Ok(r) => r, Err(SwapchainCreationError::UnsupportedDimensions) => return, Err(e) => panic!("Failed to recreate swapchain: {:?}", e), }; swapchain = new_swapchain; framebuffers = window_size_dependent_setup( &new_images, render_pass.clone(), &mut viewport, ); recreate_swapchain = false; } let (image_num, suboptimal, acquire_future) = match swapchain::acquire_next_image(swapchain.clone(), None) { Ok(r) => r, Err(AcquireError::OutOfDate) => { recreate_swapchain = true; return; } Err(e) => panic!("Failed to acquire next image: {:?}", e), }; if suboptimal { recreate_swapchain = true; } let mut builder = AutoCommandBufferBuilder::primary( device.clone(), queue.family(), CommandBufferUsage::OneTimeSubmit, ) .unwrap(); builder // Now copy that framebuffer buffer into the framebuffer image .copy_buffer_to_image(fb2d_buffer.clone(), fb2d_image.clone()) .unwrap() // And resume our regularly scheduled programming .begin_render_pass( framebuffers[image_num].clone(), SubpassContents::Inline, std::iter::once(vulkano::format::ClearValue::None) ) .unwrap() .set_viewport(0, [viewport.clone()]) .bind_pipeline_graphics(pipeline.clone()) .bind_descriptor_sets( PipelineBindPoint::Graphics, pipeline.layout().clone(), 0, set.clone(), ) .bind_vertex_buffers(0, vertex_buffer.clone()) .draw(vertex_buffer.len() as u32, 1, 0, 0) .unwrap() .end_render_pass() .unwrap(); let command_buffer = builder.build().unwrap(); let future = acquire_future .then_execute(queue.clone(), command_buffer) .unwrap() .then_swapchain_present(queue.clone(), swapchain.clone(), image_num) .then_signal_fence_and_flush(); match future { Ok(future) => { previous_frame_end = Some(future.boxed()); } Err(FlushError::OutOfDate) => { recreate_swapchain = true; previous_frame_end = Some(sync::now(device.clone()).boxed()); } Err(e) => { println!("Failed to flush future: {:?}", e); previous_frame_end = Some(sync::now(device.clone()).boxed()); } } } _ => (), } }); } fn window_size_dependent_setup( images: &[Arc<SwapchainImage<Window>>], render_pass: Arc<RenderPass>, viewport: &mut Viewport, ) -> Vec<Arc<Framebuffer>> { let dimensions = images[0].dimensions().width_height(); viewport.dimensions = [dimensions[0] as f32, dimensions[1] as f32]; images .iter() .map(|image| { let view = ImageView::new(image.clone()).unwrap(); Framebuffer::start(render_pass.clone()) .add(view) .unwrap() .build() .unwrap() }) .collect::<Vec<_>>() }
cargo run time! Let it sit and compile for a while, and then you should be able to see how it works. What happens? Why?
Activity
Add a function to draw a filled rectangle (draw_filled_rect()) and call it. Bonus: Make it bounce around on the screen like an old screensaver.
You may want to call the clear function!
Double Buffering
What happens if our code to update the framebuffer is running while the graphics adapter is copying from our memory region to the screen? Vulkano prevents us from doing this, but imagine what graphical corruption would happen! We'd have half of one image and half of another, leading to tearing at best!
This is why Vulkan gives us the swapchain, a series of buffers (at least two!) we draw into. When we're done drawing one, Vulkan flips the buffers for us, asking the adapter to display one while it draws into the next; then it flips again and repeats the process. This reduces graphical artifacts like tearing or other situations where a screen which is in between two updates is displayed.
As long as we complete our work within a single frame (if we're going at 60fps, about 16ms) this all works smoothly and the next frame is ready before the adapter needs to draw it. Think about what might happen, though, if our update takes just slightly too long (say, 18ms). Then we don't flip in time, and our next update (if it can catch up successfully) will end up skipping a frame—if we're lucky! We can even see frames being displayed for inconsistent durations, ruining the illusion of motion and potentially interfering with the simulation, depending on how the game is programmed.
The key thing to remember is that you have a frame budget and need to stay inside of it for all your input handling, updating, and drawing.
Drawing Shapes
Filled rectangles are a stack of lines, and empty rectangles are just four lines (some of which are vertical!). So let's think about how we might draw lines that are not only horizontal or vertical. I think a picture will help illustrate the key issue here:
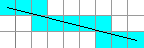
In this image, the black line is the "true" line and the grey grid represents the pixel grid over which this line is being drawn. Since we need to render to pixels, we have to color in (shaded in blue) any pixel the line overlaps. This is also called rasterization—we are converting from a vector representation of the line (its start and end points) to a raster (or grid) representation: a set of grid squares.
Note that the line just barely crosses two of the blue pixels. We might prefer that these are not included in the rendered line for aesthetic reasons, or we might shade them a very light blue to reflect the fact that they are only partially touched by the line. We won't get into antialiasing now, but we will fix the first issue. Stylistically, we'd like to ensure that we only have one colored pixel for each major step of the line (along the steeper direction of its slope). So for this line, we'd like to see only rightwards and downwards-rightwards-diagonal steps—never a vertical downwards step.
The fundamental rasterization algorithm is Bresenham's line algorithm, presented here in Rust based on the version from Wikipedia. For more detail (and for more efficient alternatives with fewer conditional checks) I suggest chapters 36 and 37 of Abrash's book.
#[allow(dead_code)] fn line(fb: &mut [Color], (x0, y0): (usize, usize), (x1, y1): (usize, usize), col: Color) { let mut x = x0 as i64; let mut y = y0 as i64; let x0 = x0 as i64; let y0 = y0 as i64; let x1 = x1 as i64; let y1 = y1 as i64; let dx = (x1 - x0).abs(); let sx: i64 = if x0 < x1 { 1 } else { -1 }; let dy = -(y1 - y0).abs(); let sy: i64 = if y0 < y1 { 1 } else { -1 }; let mut err = dx + dy; while x != x1 || y != y1 { fb[(y as usize * WIDTH + x as usize) ..(y as usize * WIDTH + (x as usize + 1))] .fill(col); let e2 = 2 * err; if dy <= e2 { err += dy; x += sx; } if e2 <= dx { err += dx; y += sy; } } }
The key idea is to walk along the line by steps based on its slope, keeping track of both our x and y positions and our accumulated error due to the fact that the slope is fractional but our steps are integral. Note that we use the sign of the change in x and y to determine which direction to walk along our line, and we use the run (change in x) and the negated rise (change in y) to determine when we need to make vertical or horizontal steps: if we have walked vertically too long (error term is larger than half the negative rise), we step horizontally and increase error by the rise term (shrinking it); if we have walked horizontally too long (error term is smaller than half the run), we step vertically and increase error by the run term. This presentation handles all slopes uniformly, but there are performance gains to be had by treating each octant, horizontal lines, and vertical lines separately—or by looking at the line as a kind of staircase of mainly horizontal (or vertical) segments.
We could probably avoid some multiplications during indexing by changing the units of y and x so that we could increase x by sx*DEPTH and increase y by sy*pitch. It's worth a try!
bitblt the ultimate
The last graphics primitive we'll talk about is drawing pre-made images, or textures. Textures are everywhere—the icons for your close/minimize/maximize buttons, your mouse cursor, and so on. They can be drawn scaled, rotated, and transformed in various ways. Sometimes a texture is backed by one image file or buffer, but sometimes a texture is laid out with other textures in memory to form an atlas. We'll talk in more detail about those when we get into animation, but for now we want to solve this problem:
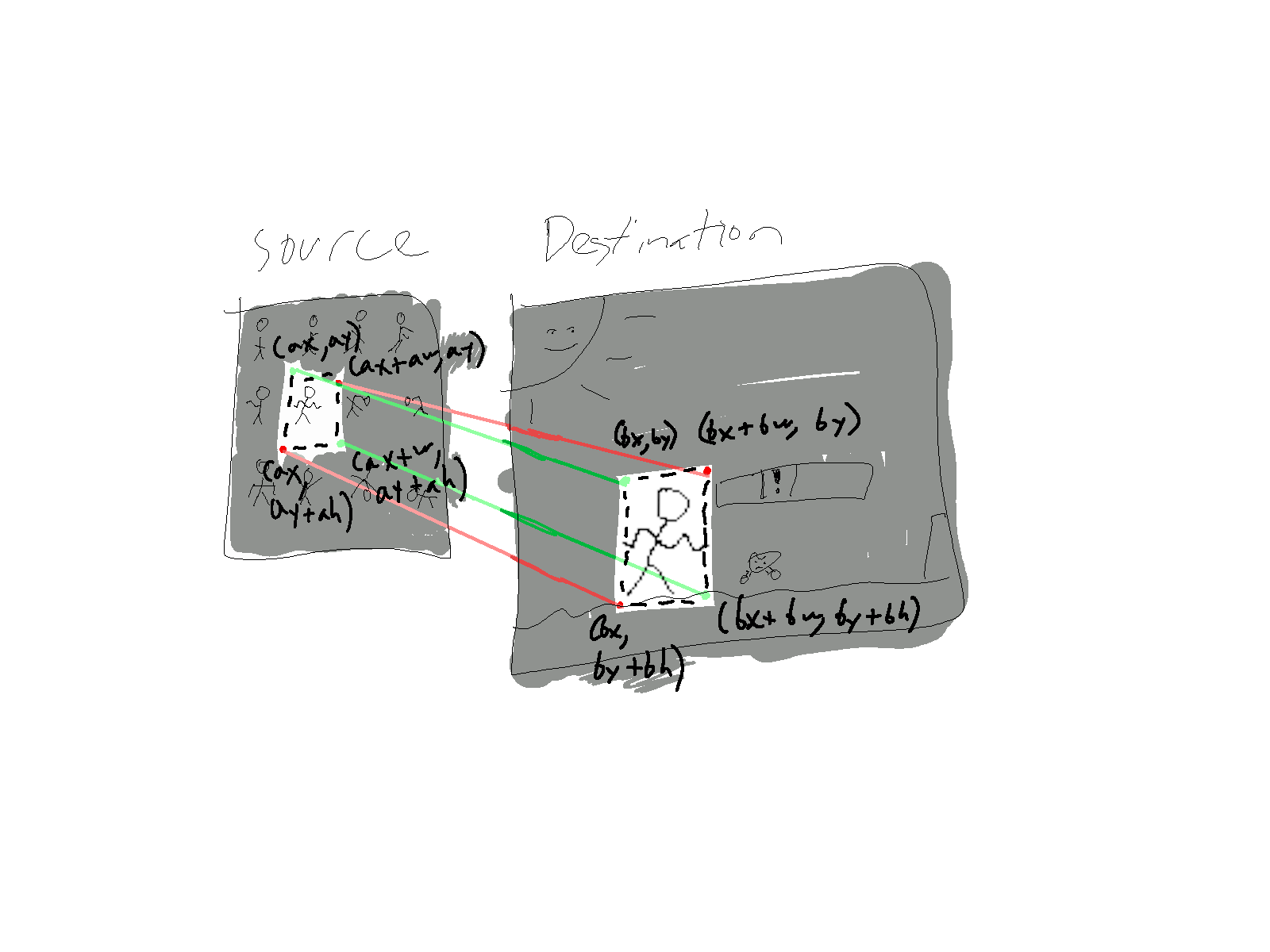
In other words, we need to draw one rectangular portion of a source texture into a portion of a destination texture, and these portions might not be the same size. This function goes by many names, but the most traditional name is probably blitting; the procedure bitblt was in many ways the foundation of graphical user interfaces back in the days of Xerox PARC and later Apple.
Bit blitting is mainly a translation problem: If we're filling the rectangle of dst rooted at \((bx,by)\) and with dimensions \(bw \times bh\) from the rectangle of src whose origin is \((ax,ay)\) and dimensions \(aw \times ah\), how do we decide which pixel of the src rect a we should use for each pixel of the dst rect b? If it weren't for scaling, all we would need to do is align their coordinate systems via translation:
for y in 0..h { for x in 0..w { // Since x and y increase in a predictable way, // it might be better to advance a dst index and a src index // independently to avoid multiplications. // You could probably even do something smart with iterators in Rust // to avoid almost all the bounds checks. dst[to_index(b.x+x, b.y+y, dst_width)] = src[to_index(a.x+x, a.y+y, src_width)]; } }
But scaling means that one dst pixel might correspond to several src pixels, or vice-versa. So we might try normalizing "how far down we are" and "how far right we are" in b, and find the corresponding point in a:
for y in 0..b.h { // You'd rather find a "step" value and increment ynorm each time let ynorm = y as f32 / b.h as f32; let ay = (ynorm * a.h as f32) as usize; for x in 0..b.w { let xnorm = y as f32 / b.h as f32; let ax = (ynorm * a.h as f32) as usize; // And you'd rather blend multiple pixels of a if a is larger, // or scale with respect to the neighborhood of ax,ay if b is larger. // This is called /interpolation/. dst[to_index(b.x+x,b.y+y,dst_width)] = src[to_index(a.x+ax,a.y+ay,src_width)]; } }
If you want to implement bitblt with scaling, get in touch and we can figure out a good way to do it! Otherwise, the version with the a and b rectangles the same size will work well much of the time.
In 3D graphics, we call a generalized version of bitblt texture mapping.
Finally, we'll show a more "real world" version of bitblt that handles transparency.
It assumes that the input image color channels are premultiplied by the alpha value, probably when they're loaded from disk.
fn bitblt(src: &Image, from:Rect, dst: &mut Image, to:Vec2) { assert!(rect_inside(from, (0,0,src_size.0,src_size.1))); let (to_x, to_y) = to; if (to_x + from.2 as i32) < 0 || (dst_size.0 as i32) <= to_x || (to_y + from.3 as i32) < 0 || (dst_size.1 as i32) <= to_y { return; } let src_pitch = src_size.0; let dst_pitch = dst_size.0; // All this rigmarole is just to avoid bounds checks on each pixel of the blit. // We want to calculate which row/col of the src image to start at and which to end at. // This way there's no need to even check for out of bounds draws--- // we'll skip rows that are off the top or off the bottom of the image // and skip columns off the left or right sides. let y_skip = to_y.max(0) - to_y; let x_skip = to_x.max(0) - to_x; let y_count = (to_y + from.3 as i32).min(dst_size.1 as i32) - to_y; let x_count = (to_x + from.2 as i32).min(dst_size.0 as i32) - to_x; // The code above is gnarly so these are just for safety: debug_assert!(0 <= x_skip); debug_assert!(0 <= y_skip); debug_assert!(0 <= x_count); debug_assert!(0 <= y_count); debug_assert!(x_count <= from.2 as i32); debug_assert!(y_count <= from.3 as i32); debug_assert!(0 <= to_x + x_skip); debug_assert!(0 <= to_y + y_skip); debug_assert!(0 <= from.0 as i32 + x_skip); debug_assert!(0 <= from.1 as i32 + y_skip); debug_assert!(to_x + x_count <= dst_size.0 as i32); debug_assert!(to_y + y_count <= dst_size.1 as i32); // OK, let's do some copying now for (row_a, row_b) in src // From the first pixel of the top row to the first pixel of the row past the bottom... [(src_pitch * (from.1 as i32 + y_skip) as usize)..(src_pitch * (from.1 as i32 + y_count) as usize)] // For each whole row... .chunks_exact(src_pitch) // Tie it up with the corresponding row from dst .zip( dst[(dst_pitch * (to_y + y_skip) as usize) ..(dst_pitch * (to_y + y_count) as usize)] .chunks_exact_mut(dst_pitch), ) { // Get column iterators, save on indexing overhead let to_cols = row_b [((to_x + x_skip) as usize)..((to_x + x_count) as usize)].iter_mut(); let from_cols = row_a [((from.0 as i32 + x_skip) as usize)..((from.0 as i32 + x_count) as usize)].iter(); // Composite over, assume premultiplied rgba8888 in src! for (to, from) in to_cols.zip(from_cols) { let ta = to.3 as f32 / 255.0; let fa = from.3 as f32 / 255.0; to.0 = from.0.saturating_add((to.0 as f32 * (1.0 - fa)).round() as u8); to.1 = from.1.saturating_add((to.1 as f32 * (1.0 - fa)).round() as u8); to.2 = from.2.saturating_add((to.2 as f32 * (1.0 - fa)).round() as u8); to.3 = ((fa + ta * (1.0 - fa)) * 255.0).round() as u8; } } }
For reference, here's a premultiply function:
enum AlphaChannel { First, Last, } fn premultiply(img: &mut [Color], alpha: AlphaChannel) { match alpha { AlphaChannel::First => { for px in img.iter_mut() { let a = px.0 as f32 / 255.0; px.1 = (*px.1 as f32 * a).round() as u8; px.2 = (*px.2 as f32 * a).round() as u8; px.3 = (*px.3 as f32 * a).round() as u8; // swap around to rgba8888 let a = px.0; px.0 = px.1; px.1 = px.2; px.2 = px.3; px.3 = a; } } AlphaChannel::Last => { for px in img.iter_mut() { let a = px.3.unwrap() as f32 / 255.0; px.0 = (px.0 as f32 * a) as u8; px.1 = (px.1 as f32 * a) as u8; px.2 = (px.2 as f32 * a) as u8; // already rgba8888 } } } }
Getting our Types in Order
In a real program we would want much better types—e.g., Rect instead of (usize, usize, usize, usize) and Vec2i instead of (i32, i32).
So let's define them:
#[derive(PartialEq, Eq, Clone, Copy, Hash, Debug)] pub struct Rect { pub x:i32, pub y:i32, pub w:u32, pub h:u32 // Float positions and extents could also be fine } impl Rect { pub fn new(x:i32, y:i32, w:u32, h:u32) -> Rect { Rect{x,y,w,h} } // Maybe add functions to test if a point is inside the rect... // Or whether two rects overlap... } #[derive(PartialEq, Eq, Clone, Copy, Hash, Debug)] pub struct Vec2i { // Or Vec2f for floats? pub x:i32, pub y:i32 } impl Vec2i { pub fn new(x:i32,y:i32) -> Vec2i { Vec2i{x,y} } // Maybe add functions for e.g. the midpoint of two vecs, or... } // Maybe add implementations of traits like std::ops::Add, AddAssign, Mul, MulAssign, Sub, SubAssign, ...
You often may find you need to pass around an image buffer with its dimensions, so a type could help us there too:
pub struct Image { pub buffer:Box<[Color]>, // or Vec<Color>, or... pub w:usize, pub h:usize } impl Image { // maybe a function to load it from a file using the png crate! // you'd want to premultiply it and convert it from `[u8]` into `[Color]`! // maybe put bitblt into here? // ... what else? // ... Could our 2d framebuffer itself be an `Image`? }
Activity: Tidying up types
Tweak the drawing functions we've seen so far to use Image, Vec2i, Rect, and our other nice types to make them more robust and easier to use.