Assignment 4: Dijkstra’s Algorithm and Data Structures
Learning Goals
- Learn how to implement graph algorithms and use an adjacency list.
- Discover properties about heaps and how they relate to other data structures.
- Apply tree balancing with a Red-Black binary search tree.
- Compare different methods for implementing hash tables.
Grading
This assignment will be graded as pass/no-pass by a TA. To pass the assignment, you must
- Complete every question in the PDF and submit your answers to gradescope.
- Complete the programming component and submit your answers to gradescope.
- Meet with your TA during your learning community sessions. I prefer both partners to be present during the walk-through, but you can each meet with the TA separately if needed.
- Walk the TA through your answers. Do not expect to make corrections during the walk-through.
- The TA will then either
- mark your assignment as 100% on gradescope, or
- inform you that you have some corrections to make.
- If corrections are needed, then you will need to complete them and conduct a new walk-through with a TA.
If you have concerns about the grading walk-through, you can meet with me after you’ve first met with a TA.
Overview
This assignment includes two parts:
- Answer the question in this PDF.
- Write a program for the problem described in section Dijkstra’s Single Source Shortest Path Algorithm (must be compatible with Python 3.8).
You may work on this assignment alone or with a partner (I much prefer you to work with a partner). Please send me a message on Slack if you want me to assign you to work with a random partner. Whether you work alone or with a partner, only one partner will submit a both parts to gradescope.
Three key points:
- you should either print the PDF and write your answers directly on the printed sheet, or add annotations to the PDF with, for example, Edge (Windows) or Preview (OSX) (using the correct format and spacing will help us grade),
- ensure that the uploading partner adds the other partners after submission, and
- if you have any questions please ask them on Slack.
Resources for the PDF Questions
For question 3(c) you can use the formula found under “Simple exponentiation” at the Wiki Page for the Birthday Problem.
For question 4, you will find the following resources fun to read:
Example Execution
I always like to start by showing you the end result.
If you do not see an animation above this line (or if you see the animation but you don’t see the progress bar), you will need to refresh the page (sometimes more than once). Or you can go directly to the player.
You can copy and past from the above animation!
Dijkstra’s Single Source Shortest Path Algorithm
Your program will accept two program arguments: (1) a filename and (2) a start vertex number. Your program will output the shortest path from the start vertex to all other vertices.
Input File
The file will include all of the information needed to create a directed graph.
The format of this file is referred to as an adjacency list. Here is an example of such a file:
1 2,1 8,2
2 1,1 3,1
3 2,1 4,1
4 3,1 5,1
5 4,1 6,1
6 5,1 7,1
7 6,1 8,1
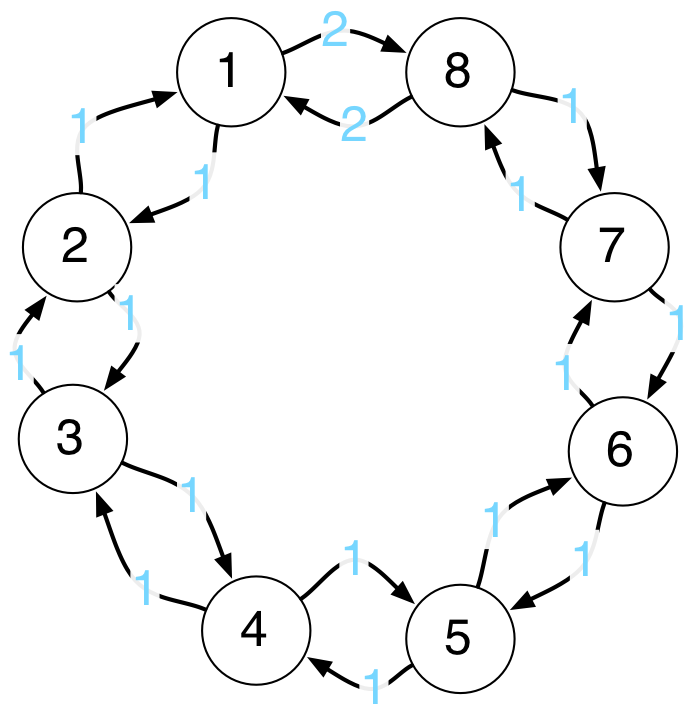
8 7,1 1,2Each line of the file contains the following information: a vertex identifier (a value from 1 through n) and then a list of edges where each edge contains a pair of values (the connecting vertex and an integer value for the edge weight).
For example, on the third line above (3 2,1 4,1) we can see that vertex 3 is connected to vertex 2 with a weight of 1, and vertex 3 is also connected to vertex 4 with a weight of 1. The graph for the above adjacency list is shown below:
Although the above example only shows two edges per node, there can be any number of edges. For example, look at the adjacency list below:
1 2,3 3,2
2 4,4
3 2,1 4,2 5,3
4 5,2 6,1
5 6,2
6 1,9Additionally, the spacing between edges might not be consistent. Your program should handle any kind of whitespace between edges (i.e., multiple spaces and tabs).
Your program
Your file must be named dijkstras.py.
You will implement Dijkstra’s Algorithm using this implementation of a Fibonacci Heap (fibheap.py). See this page created by Dr. Damon Wischik for additional help using his code.
You will need to follow these steps:
Step 1. Open the input file and read in the contents. I read the data into a Python dictionary where each key was a vertex identifier and each value was a list of edges. For instance, this is what my dictionary looks like for the example pictured above:
{
1: [(2, 1), (8, 2)],
2: [(1, 1), (3, 1)],
3: [(2, 1), (4, 1)],
4: [(3, 1), (5, 1)],
5: [(4, 1), (6, 1)],
6: [(5, 1), (7, 1)],
7: [(6, 1), (8, 1)],
8: [(7, 1), (1, 2)]
}Step 2. Implement Dijkstra’s SSSP Algorithm.
Step 3. Print all path lengths as a comma separated list. For instance, the correct output for the example graph (pictured above) starting at vertex 1 is:
0,1,2,3,4,4,3,2Submitting Your Assignment
You will submit your PDF assignment on gradescope. Only one partner should submit your PDF. The submitter will add the other partner through the gradescope interface.
To pass the autograder, your output must exactly match the expected output. Your program output should be similar to the example execution above, and the autograder on gradescope will show you the correct output if yours is not formatted properly. You can use text-compare to compare your output to the expected output and that should give you an idea if you have a misspelled word or extra space (or if I do).
Additional details for using gradescope can be found here: