CS 334
Programming Languages
Spring 2000

Lecture 6

Abstraction

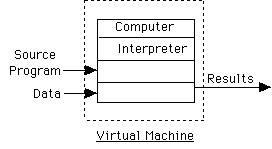
Programming language creates a virtual machine for programmer

Dijkstra: Originally we were obligated to write programs so that a computer could execute them. Now we write the programs and the computer has the obligation to understand and execute them.

Progress in programming language design marked by increasing support for abstraction.

Computer at lowest level is set of charged particles racing through wires w/ memory locations set to one and off - very hard to deal with.

In computer organization look at higher level of abstraction: interpret sequences of on/off as data (reals, integers, char's, etc) and as instructions.

Computer looks at current instruction and contents of memory, then does something to another chunk of memory (incl. registers, accumulators, program counter, etc.)

When write Pascal (or other language) program - work with different virtual machine.

Integers, reals, arrays, records, etc. w/ associated operations

Language creates the illusion of more sophisticated virtual machine.

Pure translators

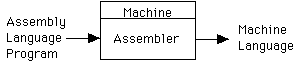
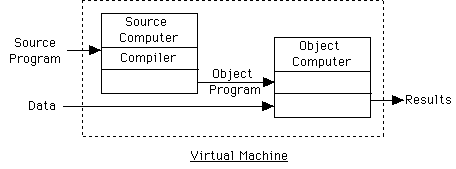
Assembler:

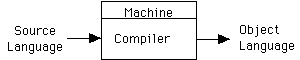
Compiler:

Preprocessor:

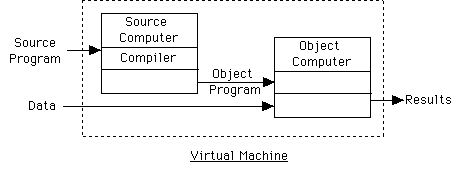
Execution of program w/ compiler:

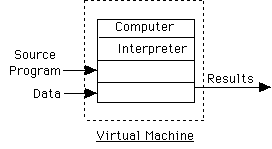
Interpreter:

We will speak of virtual machine defined by a language implementation.

Machine language of virtual machine is set of instructions supported by translator for language.

Layers of virtual machines on Mac: Bare PowerPC chip, OpSys virtual machine, Lightspeed Pascal machine, application program's virtual machine.

We will describe language in terms of virtual machine

Slight problem:

Different implementors may have different conceptions of virtual machine
Different computers may provide different facilities and operations
Implementors may make different choices as to how to simulate elts of virtual computer

May lead to different implementations of same language - even on same machine.

Problem : How can you ensure different implementations result in same semantics?

Sometimes virtual machines made explicit:

Pascal P-code and P-machine,
Modula-2 M-machine and M-code,
Java virtual machine.

Compilers and Interpreters

While exist few special purpose chips which execute high-level languages (LISP machine) most have to be translated into machine language.

Two extreme solutions:

Pure interpreter: Simulate virtual machine (our approach to run-time semantics)

    REPEAT
        Get next statement
        Determine action(s) to be executed
        Call routine to perform action
    UNTIL done

Pure Compiler:

Translate all units of program into object code (say, in machine language)
Link into single relocatable machine code
Load into memory

Comparison of Compilation vs Interpretation

compiler	interpreter
Only translate each statement once	Translate only if executed
Speed of execution	Error messages tied to source More supportive environment
Only object code in memory when executing. May take more space because of expansion	Must have interp. in memory when executing (but source may be more compact)

Rarely have pure compiler or interpreter.

Typically compile source into more easy to interpret form.
Ex. Remove white space & comments, build symbol table, or parse each line and store in more compact form (e.g. tree)

Can go farther and compile into intermediate code (e.g., P-code) and then interpret.

In FORTRAN, Format statements (I/O) are always interpreted.

Overview of structure of a compiler

Two primary phases:

Analysis:: Break into lexical items, build parse tree, generate simple intermediate code (type checking)
Synthesis:: Optimization (look at instructions in context), code generation, linking and loading.

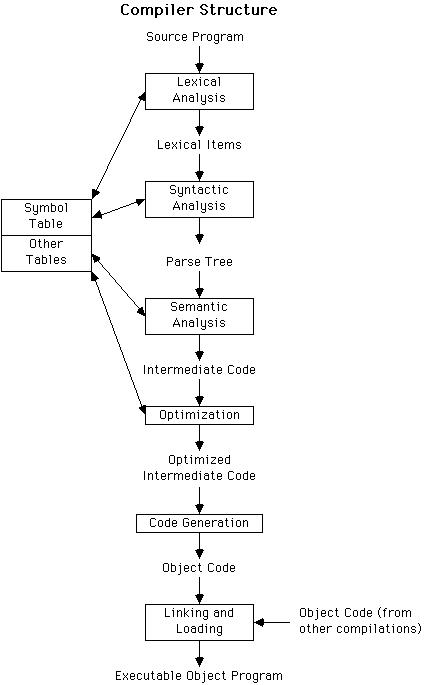
Lexical analysis:

Break source program into lexical items, e.g. identifiers, operation symbols, key words, punctuation, comments, etc. Enter id's into symbol table. Convert lexical items into internal form - often pair of kind of item and actual item (for id, symbol table reference)

Syntactical analysis:

Use formal grammar to parse program and build tree (either explicitly or implicitly through stack)

Semantic analysis:

Update symbol table (e.g., by adding type info). Insert implicit info (e.g., resolve overloaded ops's - like "+"), error detection - type-checking, jumps into loops, etc. Traverse tree generating intermediate code

Optimization:

Catch adjacent store-reload pairs, eval common sub-expressions, move static code out of loops, allocate registers, optimize array accesses, etc.
Example:

   for i := .. do ...
       for j:= 1 to n do
           A[i,j] := ....

Code generation:

Generate real assembly or machine code (now sometimes generate C code)

Linking & loading:

Get object code for all pieces of program (incl separately compiled modules, libraries, etc.). Resolve all external references - get locations relative to beginning location of program. Load program into memory at some start location - do all addressing relative to base address.

Symbol table: Contains all identifier names, kind of id (vble, array name, proc name, formal parameter), type of value, where visible, etc. Used to check for errors and generate code. Often thrown away at end of compilation, but may be held for error reporting or if names generated dynamically.

Like to have easily portable compilers front-end vs back-end

Front-end generate intermediate code and do some peep-hole optimization

Back-end generate real code and do more optimization.

Semantics

Meaning of a program (once know it is syntactically correct).

Operational semantics for most of course.
How would an interpreter for the language work on virtual machine?

Work with virtual (or abstract) machine when discuss semantics of programming language constructs.

Represent Code and Data portions of memory
Has instruction pointer, ip , incremented by one after each command if not explicitly modified by the instruction.

Run program by loading it into memory and initializing ip to beginning of program

Official language definitions: Standardize syntax and semantics - promote portability.

All compilers should accept the same programs (i.e. compile w/o errors)
All legal programs should give the same answers (modulo round-off errors, etc)
Designed for compiler writers and as programmer reference.

Often better to standardize after experience. -- Ada standardized before a real implementation.

Common Lisp, Scheme, ML now standardized, Fortran '9x.

Good formal description of syntax, semantics still hard.

Backus, in Algol 60 Report promised formal semantics.

Said forthcoming in few months - still waiting.
Years after introduction still problems and ambiguities remaining.

Specifying an interpreter with "natural semantics"

Semantics given in style of "natural semantics". Kind of operational semantics.

"e => v" means that when "e" is evaluated, it should return the value "v".

E.g. First few rules say nothing to do with simple values and function names:

n => n for n an integer.
true => true, and similarly for false
error => error
succ => succ, and similarly for the other initial functions.

Therefore if encounter simple value or function name, just return it - no further evaluation is possible. Think of these as base cases for the interpreter.

More interesting rules say that in order to evaluate a complex expression, first evaluate particular parts and then use those partial results to get the final value.

Look at following rule:

		b => true         e1 => v
	(5)	---------------------------
		if b then e1 else e2 => v

We read the rule from the bottom up: if the expression is an if-then-else with components b, e1, and e2, and b evaluates to true and e1 returns v, then the entire expression returns v. Of course, we also have the symmetric rule

		 b => false        e2 => v
	(6)	----------------------------
		 if b then e1 else e2 => v

Thus if we wish to evaluate an expression of the form "if b then e1 else e2" then first evaluate "b". If b evaluates to true, then, using rule (5), evaluate e1 to get some value, v. Return the value, v, as the final value of the "if" expression. If b evaluates to false, then use rule (6) and return the value of e2.

The application rules in homework 3 are similar. Essentially, evaluate the function. If it evaluates to one of the primitive functions, evaluate the argument and return the result of applying the primitive function to the value of the argument. Thus, the actual rule to be used is determined by the value of the function.

The following is an example which shows why you must evaluate the function:

	(if false then succ else pred) (pred 7)

The function evaluates to pred and the argument evaluates to 6. Using rule (8) from the homework, this should evaluate to 5.

Back to:

CS 334 home page

Kim Bruce's home page

CS Department home page

kim@cs.williams.edu

CS 334 Programming Languages Spring 2000 Lecture 6