CS 062, Lecture 40
Binary Search Trees (continued)
Red-Black Trees
Red-black trees also maintain balance, but restructuring only O(1) after
an update.
A red-black tree is a binary search tree with nodes colored red and black
in a way that satisfies the following properties:
- The root is black.
- Every external node is black.
- The children of a red node are black. (I.e., no two consecutive
red nodes on a path.)
- All the external nodes have the same black depth -- # of black
ancestors.
Here is a simple example:

Proposition: The height of a red-black tree storing n entries is O(log
n). In fact, log(n+1) <= h <= 2 log(n+1).
The idea behind this is if we erase the red nodes then the tree will be
perfectly balanced. Hence the black height = log (# black nodes). The
red nodes can at most double the length of a path.
Insertion in a red-black tree:
- If insert at root, then color it black.
- Otherwise insert as usual, but color new node red.
If now have two red nodes in a row, must restructure. All other properties
are OK. Suppose just added n, but n's parent p is also red. Then p's
parent g must be black. What we do next depends on p's sibling, u:
- p's sibling, u, is black (and may be external)
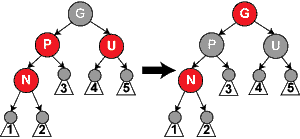
If n and p are opposite children (one is left and the other is right),
then perform a rotation that moves n up to p's place in the tree (and p
moves down). Notice that this does not change the black depth of any
external node. Now they are both right children or both left
children.
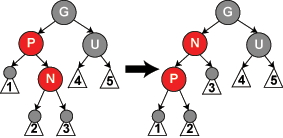
Now that n and p are both the same kind of child then rotate around
grand parent g so that p is now at the root of the subtree. Now change
the colors of p and g so that n and g are now both red. Notice that u
is the child of g and black (because we had no prior conflicts). It is
easy to verify that we have fixed the double red problem and not
changed any other paths. Also notice that the black depth of each
external node is the same as in the original.
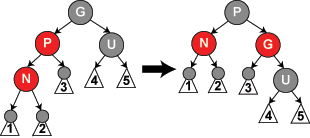
- p's sibling, u, is red. Flip the colors of p and u to be black,
and g to be red. This preserves other properties, but may require
further work if g's parent is also red. If so, keep going recursively
until there are no pairs of red or until reach root. If root is ever
red, just change to black and stop. Notice that the black depth of all
external nodes are the same as before.
Deletion can be handled similarly, though the details are a bit
complicated. See the text or the wikipedia article on red-black trees. See
also the red
black tree demo on-line.
The main advantage of red-black trees over AVL is that they need fewer
rotations, so in practice will be a bit faster. However, algorithms are
considerably more complex, so AVL easier to explain.
The pictures in these lecture notes are from the wikipedia article on
red-black trees.
Splay Trees
Idea behind splay tree. Every time find, get, add, or remove an element x,
move it to the root by a series of rotations.
Splay means to spread outwards
- if x is root, done.
- if x is left (or right) child of root, rotate it to the root
- if x is left child of p, which is left child of g, do right
rotation about g and then about p to get x to grandparent position.
(Similarly for double right grandchild). Continue splaying until at
root.
- if x is right child of p, which is left child of g, then rotate
left about p and then right about g. (Similarly for left child of
right child of g) Continue splaying until at root.
Tree can get more unbalanced w/ splay operations, but ave depth of nodes on
original path is (on average) cut in half. Therefore if repeatedly look
for same elts, then will find much faster (happens in practice).
Implemented as a specialization of binary search tree - same interface, but when perform
insert or search, splay the elt. When remove an elt, splay its
parent.
If more recently accessed elements are more likely to be accessed then
this can be a big win, but lose big if each uniformly likely to be
accessed, though on average gives O(log n) behavior. Note that needs no
extra info at nodes.
Sets
So far we have seen two ways in which we can represent sets
- Bitstrings
- Hash tables
Bitstrings are very fast and easy and support set operations using the
usual bit operations of & (for intersection), | (for union) and ~ (for
complement). Set subtraction, A-B, can also be supported by a combination
of these operations (left as an exercise for the reader).
Unfortunately we need a discrete linear ordering for this to work (e.g.,
every element has a unique successor), and in fact they all need to be
codeable as non-negative integers. Thus this works well for subranges of
ints, for chars, and for enumerated types. However, they will not work
well for strings or for other complex orderings.
Hash tables work well for representing elements when we have a good hash
table, but they don't support the set operations well at all. Taking a
union or intersection would involve traversing through all of the
elements of a hash table (empty and non-empty) to process individual
elements. This is O(N) for the size of the table, which is usually larger
than O(n) (actually, we ignore constants with "O", but you know what I
mean!).
A simple alternative is to use an ordered sequence (e.g., an ordered
linked list). It is easy to see how we could perform union, intersection,
and set subtraction operations. If moving to the next element, comparing,
and copying are all O(1) then the entire thing will be O(n+m) where n and
m are the sizes of the sets involved.
See design pattern in text for Template Method Pattern. See code on-line
in OrderedListSet.



