The array, data[0..n-1], holds the values to be stored in the tree. It does not contain references to the left or right subtrees.
Instead the children of node i are stored in positions 2*i +1 and 2*i + 2, and therefore the parent of a node j, may be found at (j-1)/2
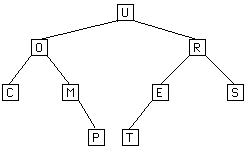
The following example shows how a binary tree would be stored. The notation under the tree is a "parenthesis" notation for a tree. A tree is represented as (Root Left Right) where Root is the value of the root of the tree and Left and Right are the representations of the left and right subtrees (in the same notation). Leaves are represented by just writing their value. When a node has only one subtree, the space for the other is filled with () to represent the absence of a subtree.

Ex. (U (O C (M () P) ) (R (E T () ) S) )
IndexRange: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 data[]: U O R C M E S - - - P T - - -
Save space for links, but it is possible that there is exponentially much wasted storage:
Storing a tree of height n requires an array of length 2n - 1 (!), even if the tree only has O(n) elements. This makes this representation very expensive if you have a long, skinny tree. However it is very efficient for holding full or complete trees.
Def: A Min-Heap H is a complete binary tree such that
This is equivalent to saying that H[i] <= H[2*i+1], H[2*i+2] for all approp values of i in the array representation of trees. Another way of looking at Min-Heap is that any path from a leaf to the root is in non-ascending order.
Notice that this heap is NOT the same as heap memory in a computer!
This turns out to be exactly what is needed to implement a priority queue.
A priority queue is a queue in which the elements with lowest priority values are removed before elements with higher priority. Entries in the priority queue have both key and value fields and their priorities are based on an ordering of the key fields. [Note that java.util.PriorityQueue is different!]
The code for priority queues referred to below can be found on-line.
One can implement a priority queue as a variation of the implementation of a regular queue where either you work harder to insert or to remove an element (i.e. store in priority order, or search each time to remove lowest priority elements).
Unfortunately, in these cases either adding or deleting an element will be O(n). (Which one is O(n) depends on which of the two schemes is adopted!)
Can provide more efficient implementation with heap!
- remove element with lowest priority (at root of tree) and then remake heap.
Ex.
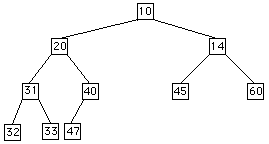
Note: In a heap - if a node has only 1 child, it must be a left child.
IndexRange: 0 1 2 3 4 5 6 7 8 9 10 data: 10 20 14 31 40 45 60 32 33 47 -
Example: Insert 15 into the heap above.
Example: Delete root in the above example.
These are exactly what are needed to implement add and remove methods for priority queue! See code in PriorityQueueWithHeap (follow link above).
When you add a new element in a priority queue, copy it into the next free position of the heap and percolate it up into its proper position.
When you remove the next element from the priority queue, remove the element from the root of heap (first elt, since it has lowest number for priority), move the last element up to the first slot, and then move it down.
How expensive are percolateUp and downHeap?
Each are log n. This compares very favorably with holding the priority queue as regular queue and inserting new elements into the correct position in the queue and removing them from the front or the alternative of not holding them in order but searching each time for the highest priority.
(log 1) + (log 2) + (log 3) + ... + (log n) = O(n log n) compares.
Traversal is O(n). Total cost is O(n log n) in both the best and average cases.
The worst case is if the list is in order, it then behaves more like an insertion sort, creating a tree with one long branch. This results in a tree search as bad as O(n2).
The heap sort described below is always better - since it automatically keeps the tree in balance.
Once the heap is established remove elements one at a time, putting smallest at end, second smallest next to end, etc.
In detail:
Swap top with last element, sift down, do heap sort on remaining n-1 elements.
Ex. 25, 46, 19, 58, 21, 23, 12
// Create a priority queue with entries from list entry ordered
// with comparator compar on K
// post: entry will have heap ordering according to compar
public PriorityQueueWithHeap(ArrayList<Entry<K,V>> entry,
Comparator<K> compar) {
heap = entry;
comp = new DefaultComparator<K>();
for (int index = parent(heap.size()-1); index >= 0; index--){
downHeap(index);
}
}
public static <K,V> ArrayList<Entry<K,V>>
heapSort(ArrayList<Entry<K,V>> elts, Comparator<K> comp) {
PriorityQueueWithHeap<K,V> pq =
new PriorityQueueWithHeap<K,V>(elts,comp);
// Extract the elements in sorted order.
ArrayList<Entry<K,V>> sorted = new ArrayList<Entry<K,V>>();
while (!pq.isEmpty()) {
try {
sorted.add(pq.removeMin());
} catch (EmptyPriorityQueueException e) {
System.out.println("logical error in heapsort");
e.printStackTrace();
}
}
return sorted;
}
If we used an array, rather than an ArrayList in the implementation, we
could do it in place by just putting removed element in last open slot in
the array.
Each sift down takes <= log n steps.
Therefore total compares <= (n/2) log n + n log n = O(n log n), in worst case. Average about same.
No extra space needed!
Actually, with a little extra work we can show that the initial "heapifying" of the list can be done in O(n) compares. The key is that we only call SiftDown on the first half of the elements of the list. That is, no calls of SiftDown are made on subscripts corresponding to leaves of the tree (corresponding to n/2 of the elements). For those elements sitting just above the leaves (n/4 of the elements), we only go through the loop once (and thus we make only two comparisons of priorities). For those in the next layer (n/8 of the elements) we only go through the loop twice (4 comparisons), and so on. Thus we make 2*(n/4) + 4*(n/8) + 6*(n/16) + ... + 2*(log n)*(1) total comparisons. We can rewrite this as n*( 1/21 + 2/22 + 3/23 + ... + log n/2log n). (Of course in the last term, 2log n = n, so this works out as above.) The sum inside the parentheses can be rewritten as Sum for i=1 to log n of (i/2i). This is clearly bounded above by the infinite sum, Sum for i=1 to infinity of i/2i. With some work the infinite sum can be shown to be equal to 2. (The trick is to arrange the terms in a triangle:
1/2 + 1/4 + 1/8 + 1/16 + ... = 1
1/4 + 1/8 + 1/16 + ... = 1/2
1/8 + 1/16 + ... = 1/4
1/16 + ... = 1/8
... = ..
-------------------------------
Sum for i=1 to infinity of i/2i = 2
Thus n*( 1/21 + 2/22 + 3/23 + ... + log
n/2log n) <= 2n, and hence the time to heapify an array is
O(n).
Low overhead makes it perform well on average.
On random data heapsort is somewhat slower than Quicksort and MergeSort. If you only need the first few items in a sorted list, it can be better since the initial heapify can be done in time O(n).
On random data somewhat slower than Quicksort.
Selection sort least affected since # copies is O(n), for rest is same as # compares.